第七章 堆和优先队列

堆和优先队列（Heap and Priority Queue）

1. 堆（Heap）

  • 堆的定义

堆是一种特殊的树。如果一个树的每一个节点元素值都大于等于（或者小于等于）它的所有子节点的元素值，且该树为完全树，则该树为最大堆（或者最小堆）。所以堆的结构必须是完全二叉树的结构。堆通过构建满足其性质的二叉树来实现。因此我们需要解释一下什么是完全二叉树。即一个二叉树，除了最底层，其他层的节点位置都被填满，且最底层尽可能地从左到右填入。

下面给出一组完全二叉树的例子。因为完全二叉树的定义只与树的结构有关而与节点的元素值无关，所以下面的完全二叉树示意图隐去的节点的元素值。

这是只有一个节点的完全二叉树。

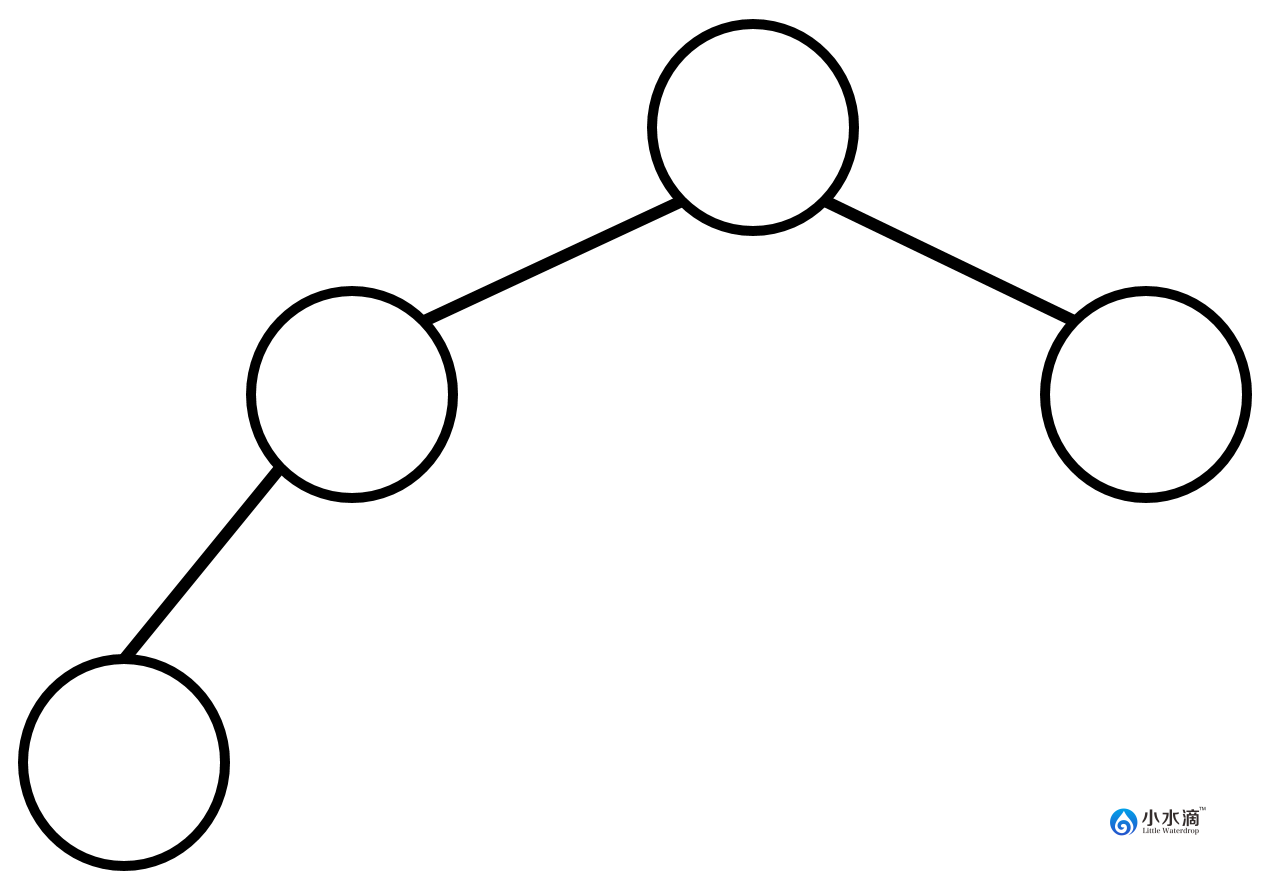
avatar

下图是一棵完全二叉树。因为第一层和第二层所有节点位置都被填满，第三层节点的位置尽可能的从左向右填充。

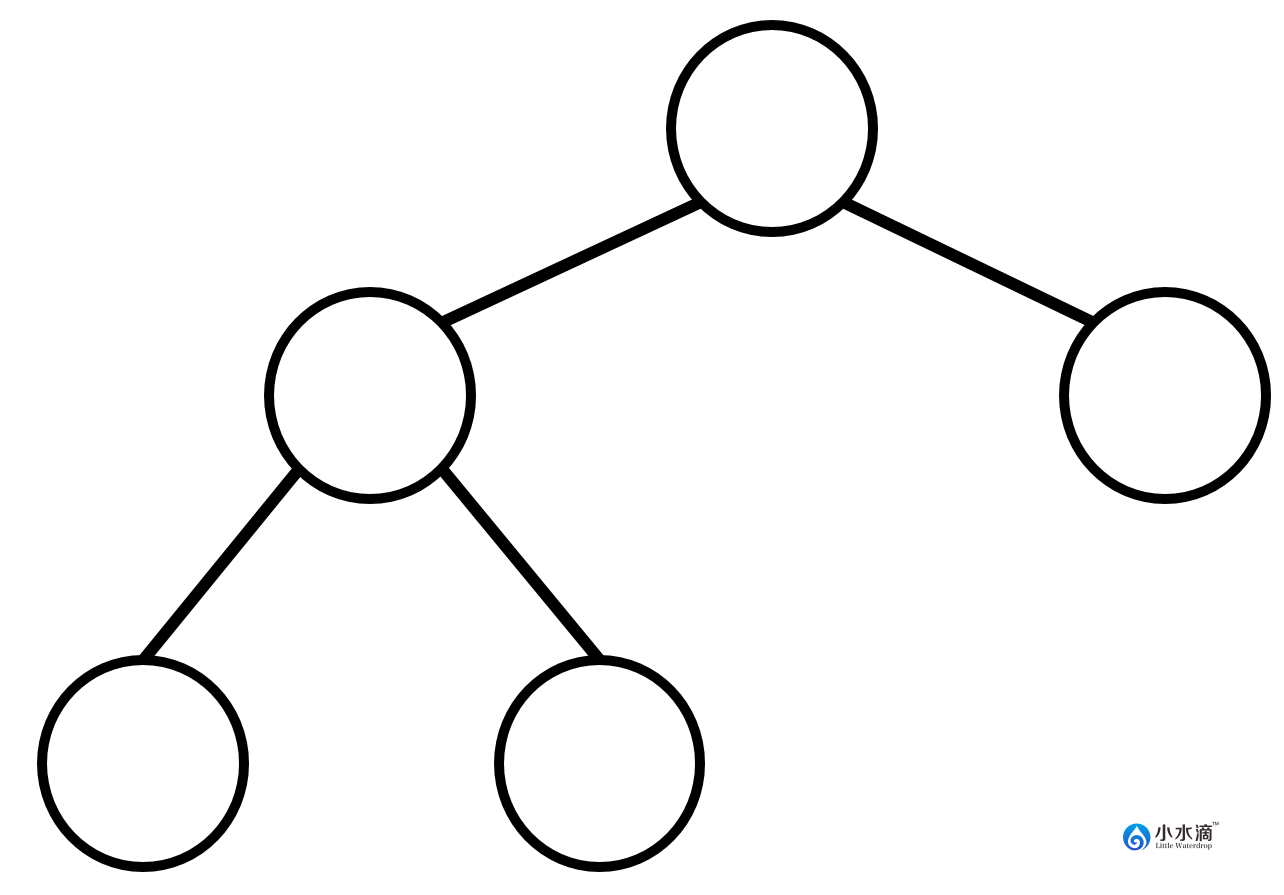
avatar

下图是一棵完全二叉树。因为第一层和第二层所有节点位置都被填满，第三层节点的位置尽可能的从左向右填充。

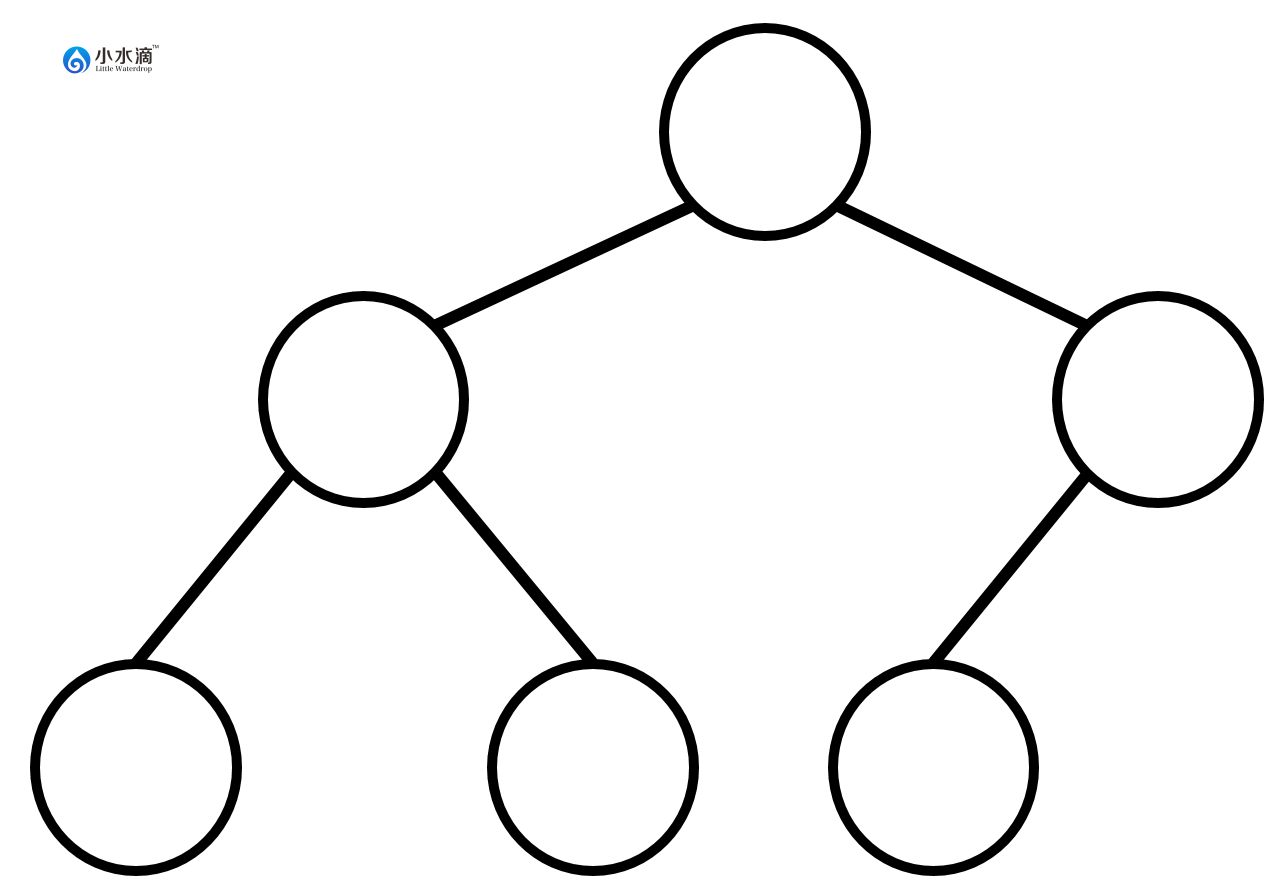
avatar

下图是一棵完全二叉树。因为第一层和第二层所有节点位置都被填满，第三层节点的位置尽可能的从左向右填充。

avatar

下图是一棵完全二叉树。因为第一层和第二层所有节点位置都被填满，第三层节点的位置尽可能的从左向右填充。该树也是一棵满二叉树，即所有节点位置都被填满。

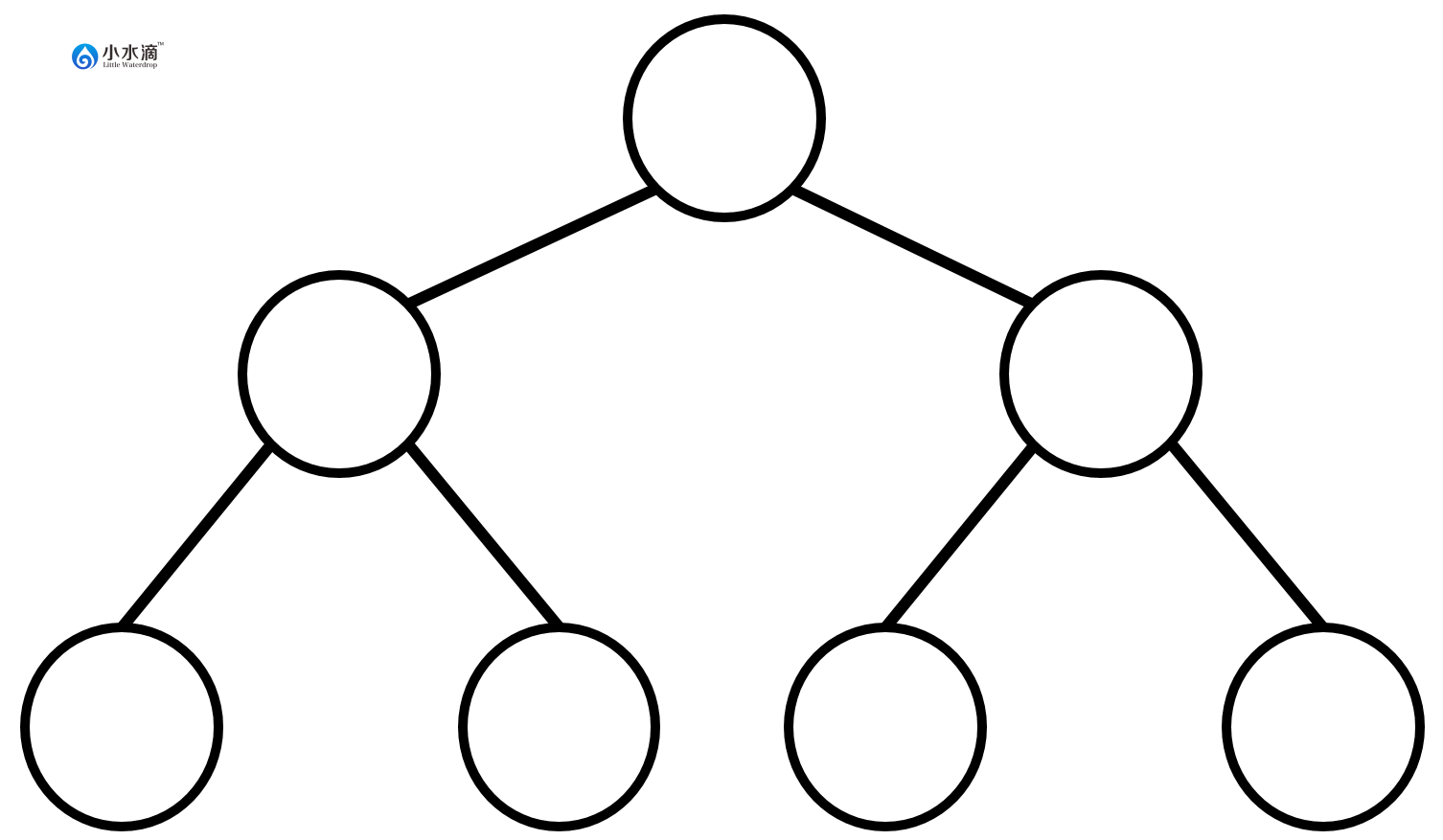
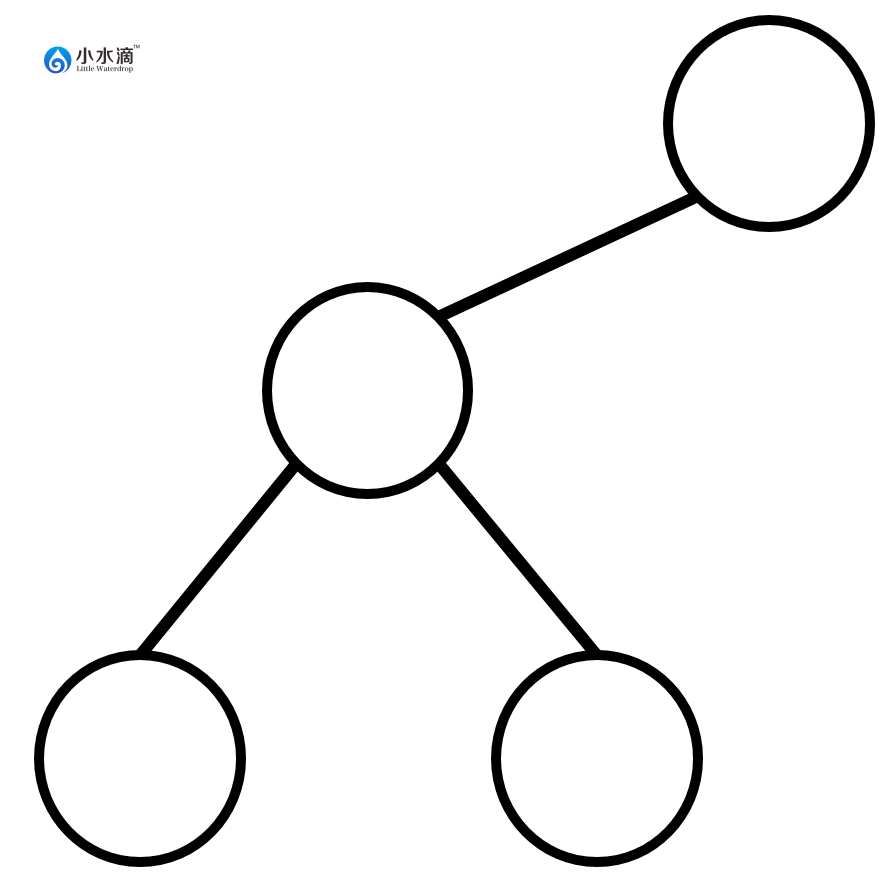
avatar

下图是一棵不完全二叉树。因为尽管第一层和第二层所有节点位置都被填满，第三层节点的位置没有尽可能的从左向右填充。

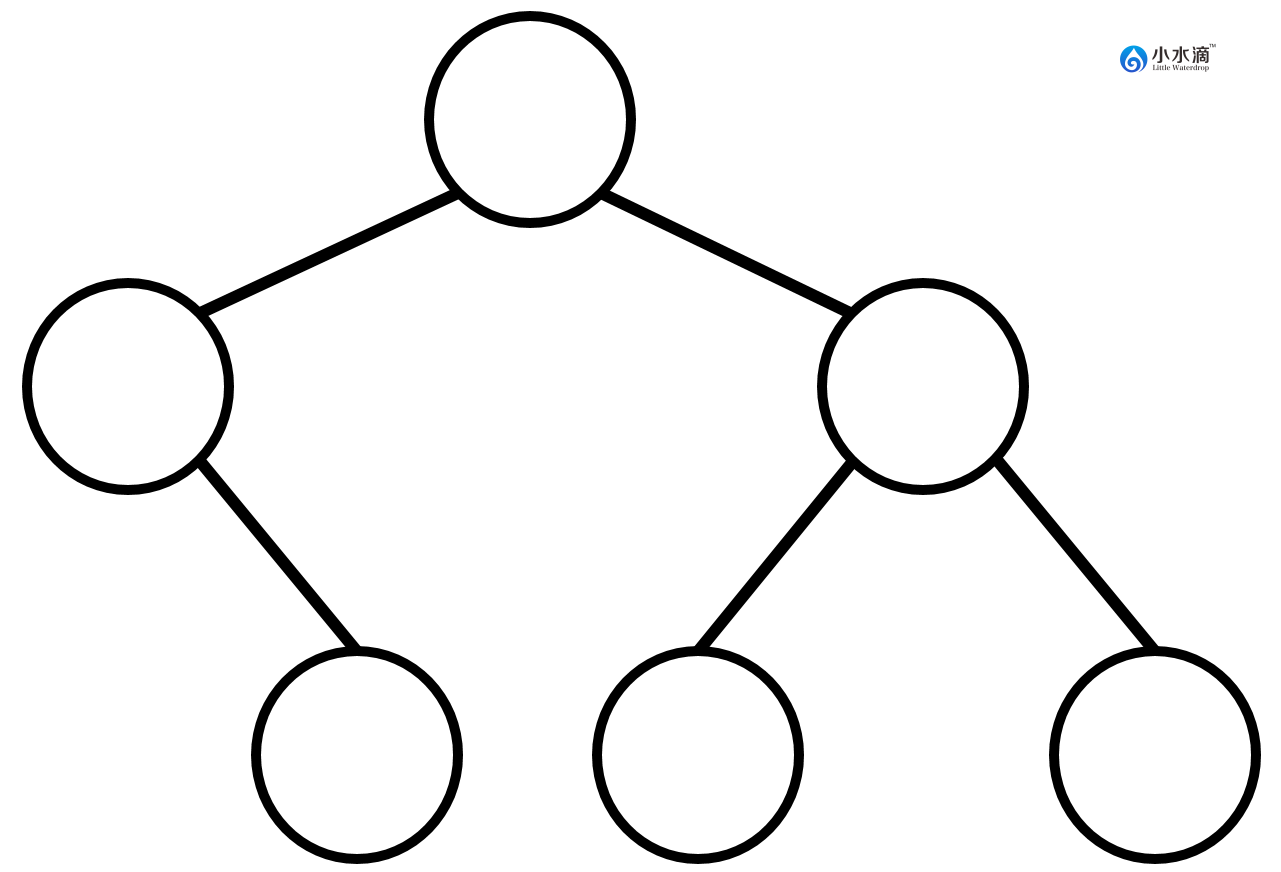
avatar

下图是一棵不完全二叉树。因为尽管第一层和第二层所有节点位置都被填满，第三层节点的位置没有尽可能的从左向右填充。

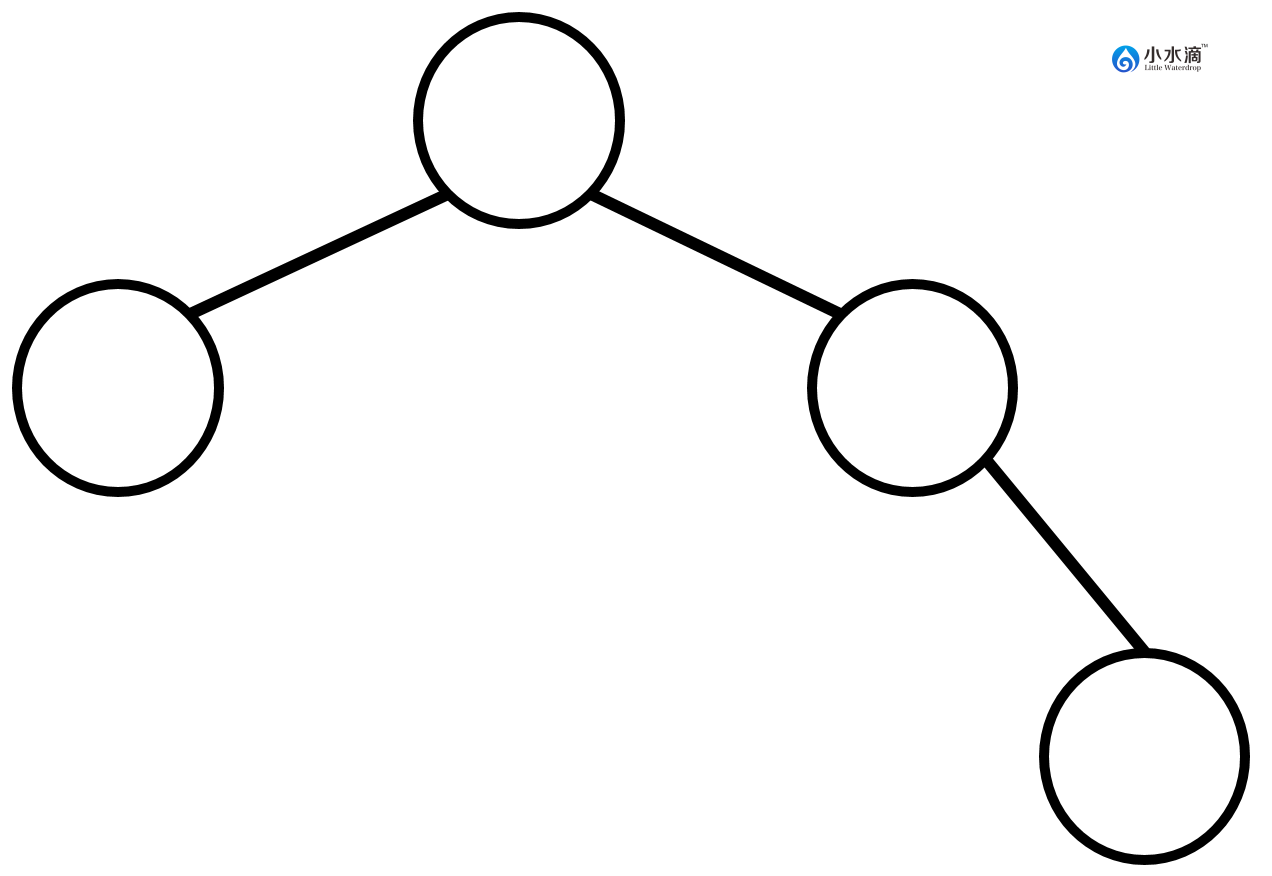
avatar

下图是一棵不完全二叉树。因为尽管第一层和第二层所有节点位置都被填满，第三层节点的位置没有尽可能的从左向右填充。

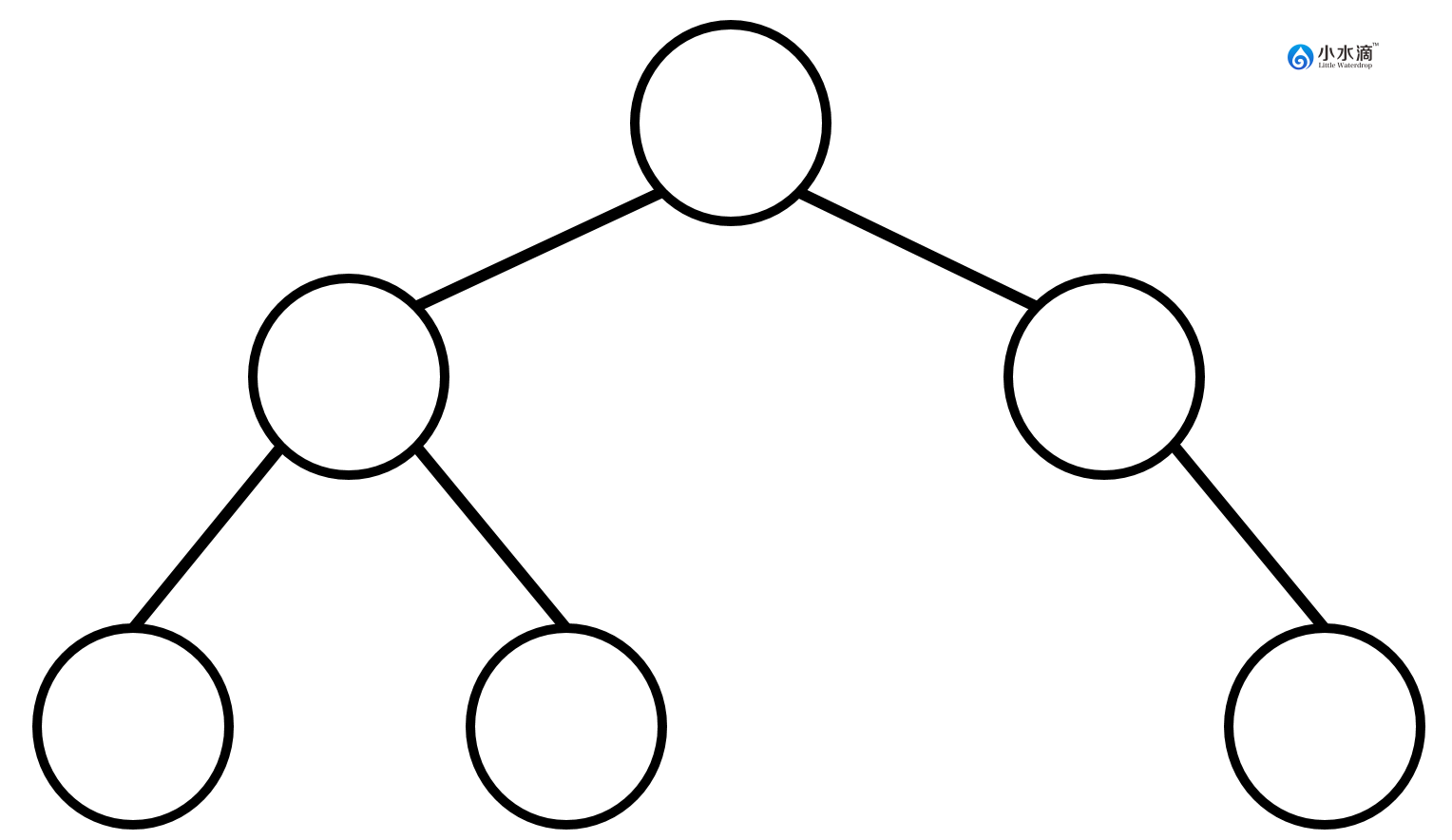
avatar

下图是一棵不完全二叉树。因为尽管第一层和第二层所有节点位置都被填满，第三层节点的位置没有尽可能的从左向右填充。

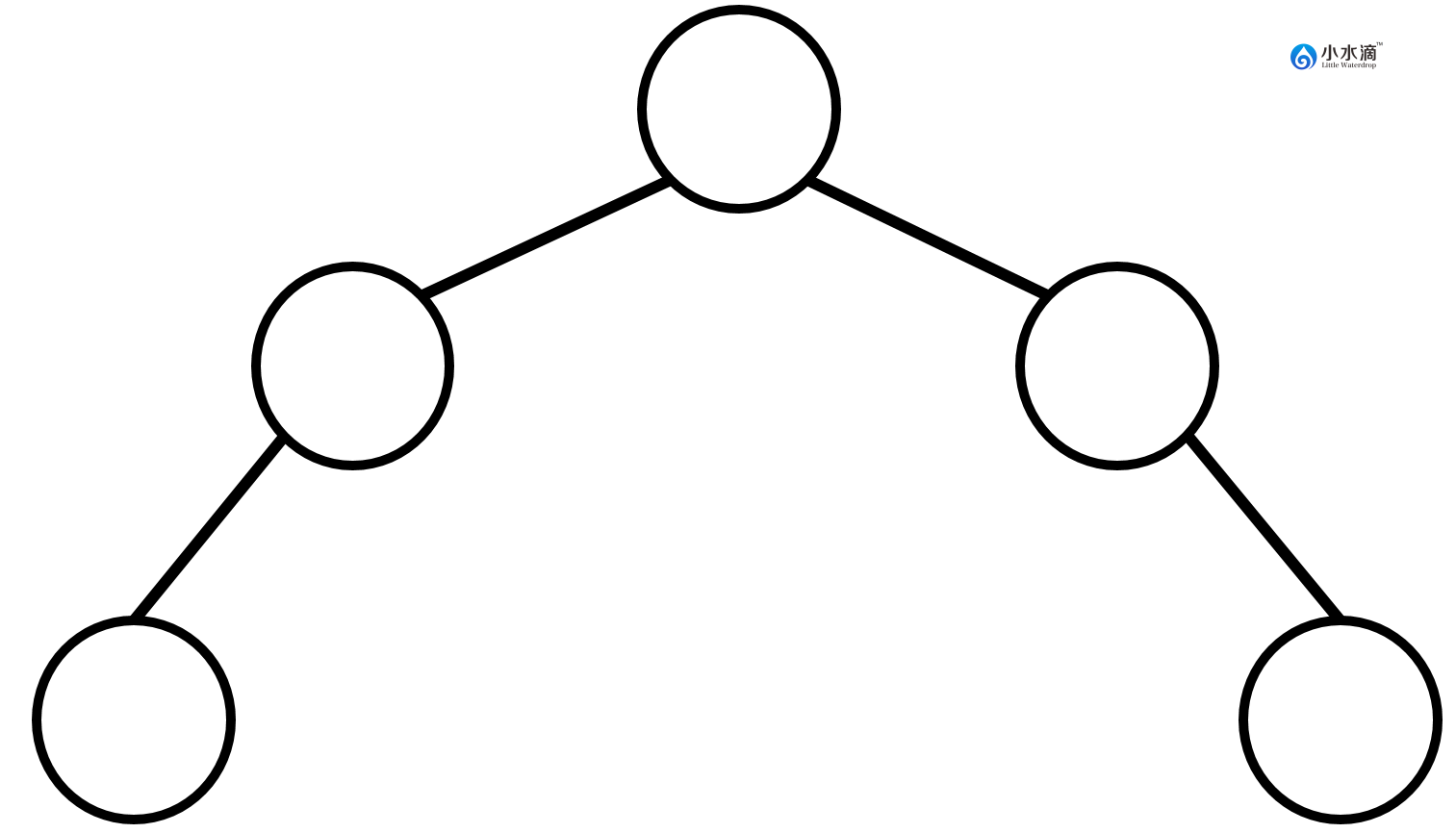
avatar

下图是一棵不完全二叉树，因为在有第三层的情况下第二层的节点位置没有填满。

avatar

  • 堆的实现和基本操作

    在完全二叉树中，任意两个有同样节点数量的完全二叉树必有完全相同的树形结构。即除最底层外，其他层有着同样数量的节点（个） ， 为该层的深度。所以我们只要知道了从上到下，从左到右的节点顺序就能表示出一个完全二叉树。因为堆必须是完全二叉树的性质，我们可以用数组来存储堆。

    下图是一个最大堆。可以看出每个节点的元素值都大于其所有子节点，且该树为一个完全二叉树。

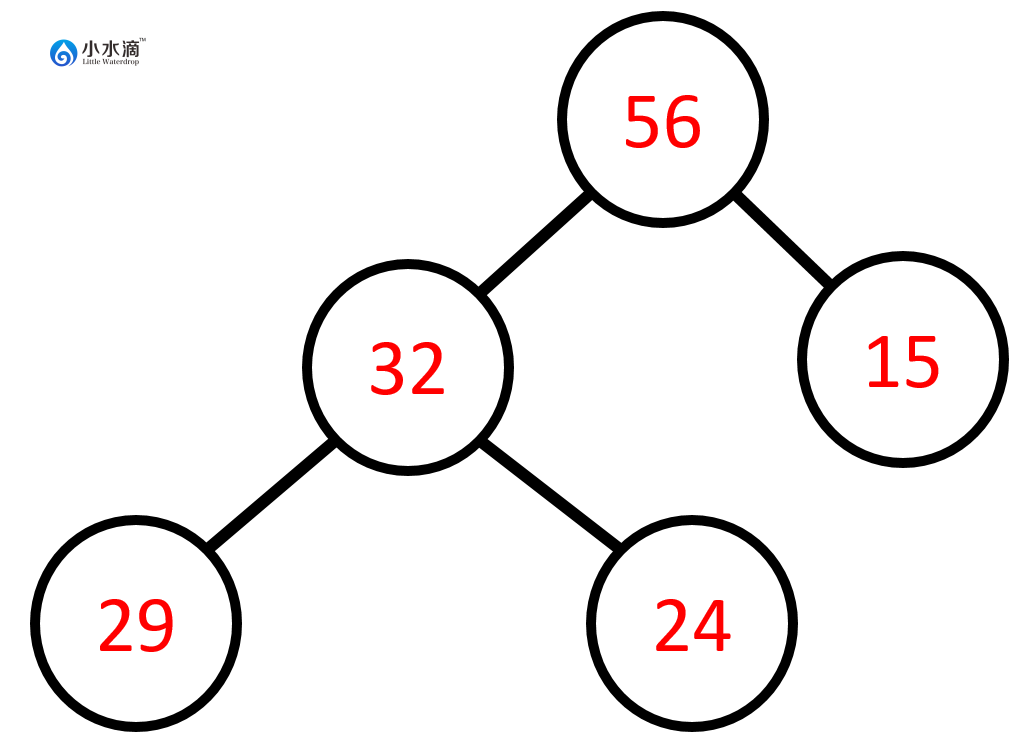
    avatar

    该堆可以存入下面的数组。

    avatar

    如果构建一个最小堆，则每个节点的元素值都应小于其所有子节点。在下面的代码中，我们用Java语言构建了一个最小堆（尚未添加基本操作）。在下面的代码里可以看出，最小堆本质上是一个数组。本例中使用的是一个整型（int）数组。

    查看和下载源代码 
      public class MinHeap {
      private int[] heap;
      private int size;
      private int maxSize;
      public MinHeap(int max_size) {
          maxSize = max_size;
          heap = new int[maxSize];
          size = 0;
      }
      
      public MinHeap() {
          maxSize = 10;
          heap = new int[maxSize];
          size = 0;      
      }  

      
      private int getParentIndex(int currentIndex) { 
          // 根据当前节点在数组中的位置计算其父节点的数组位置。
          return currentIndex / 2; 
      } 
      
      private int getLeftChildIndex(int currentIndex) { 
          // 根据当前节点在数组中的位置计算其左子节点的数组位置。
          return (2 * currentIndex); 
      } 
      
      private int getRightChildIndex(int currentIndex) { 
          // 根据当前节点在数组中的位置计算其子右节点的数组位置。
          return (2 * currentIndex) + 1; 
      } 
  }

    • 插入（insert）

      最小堆的插入操作步骤如下。

      1. 将新元素存在数组里现有的最后一个元素之后。
      2. 如果新元素值小于其父节点元素值，则二者在数组中（本质上也是在堆中）互换位置。重复该步骤直到新元素的值大于当前父节点。

      在下面的动图所示的例子中，9，8，7，6，5，4六个数字依次插入一个最小堆中。每次插入的结果如动图所示。

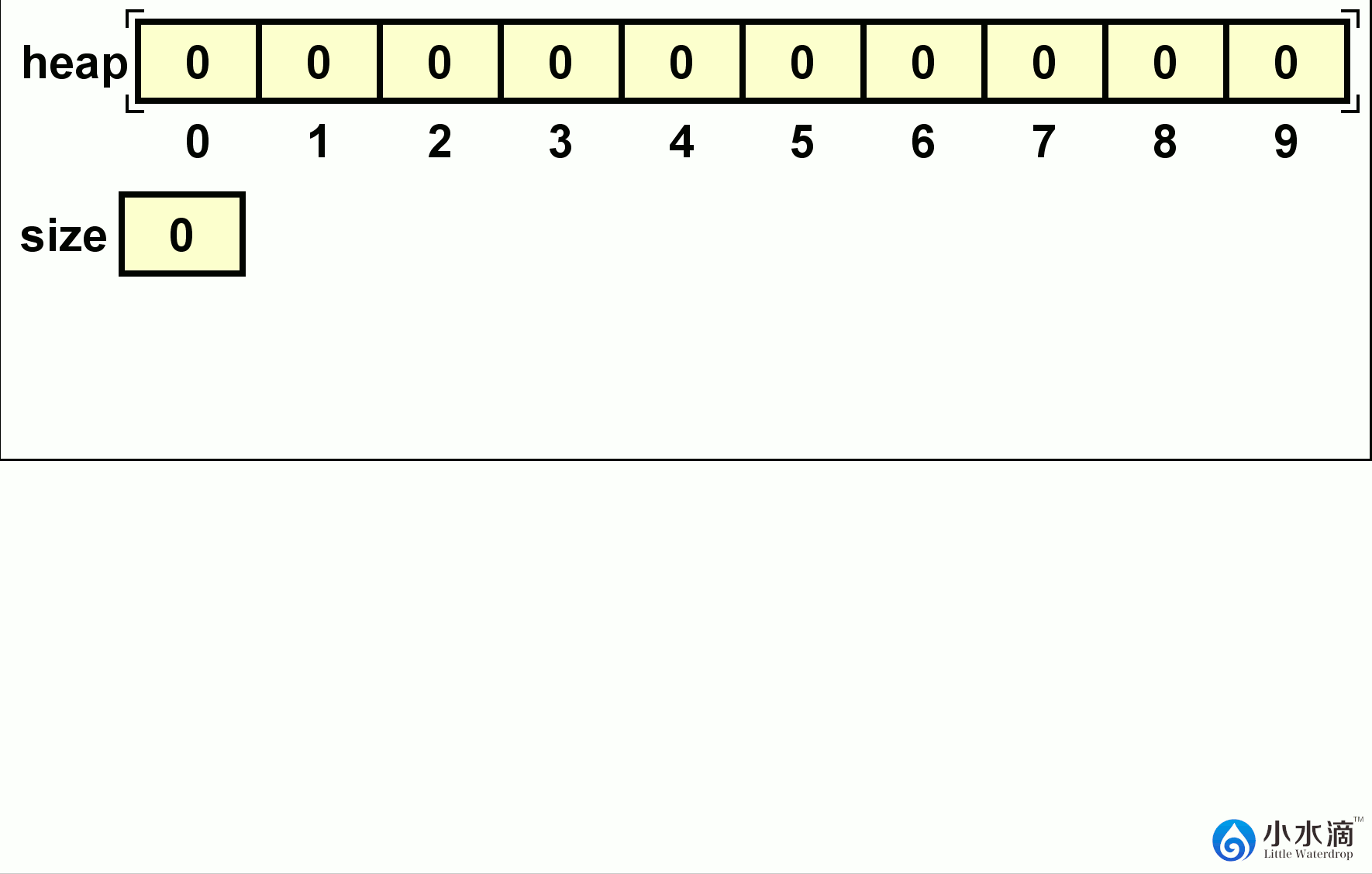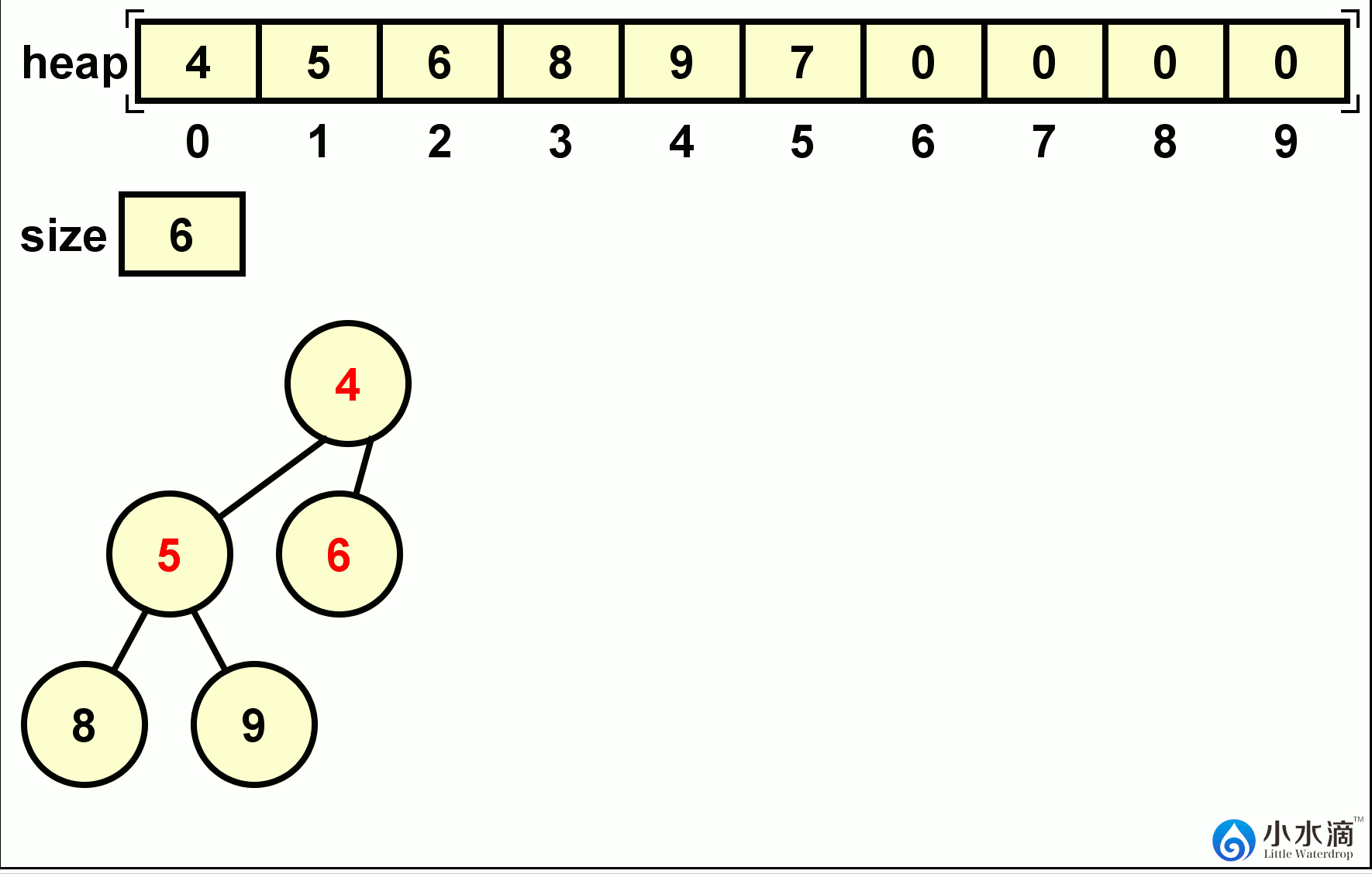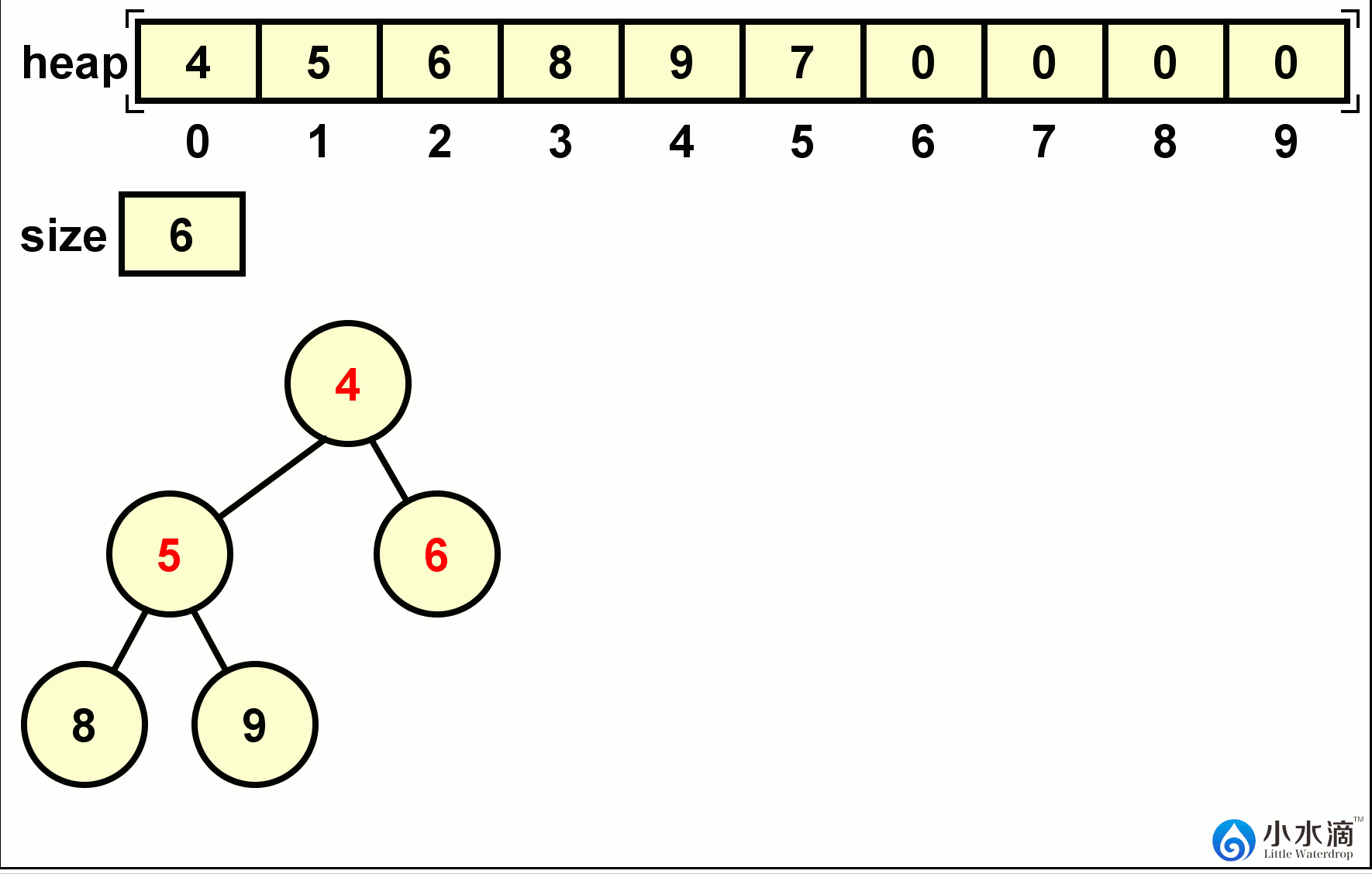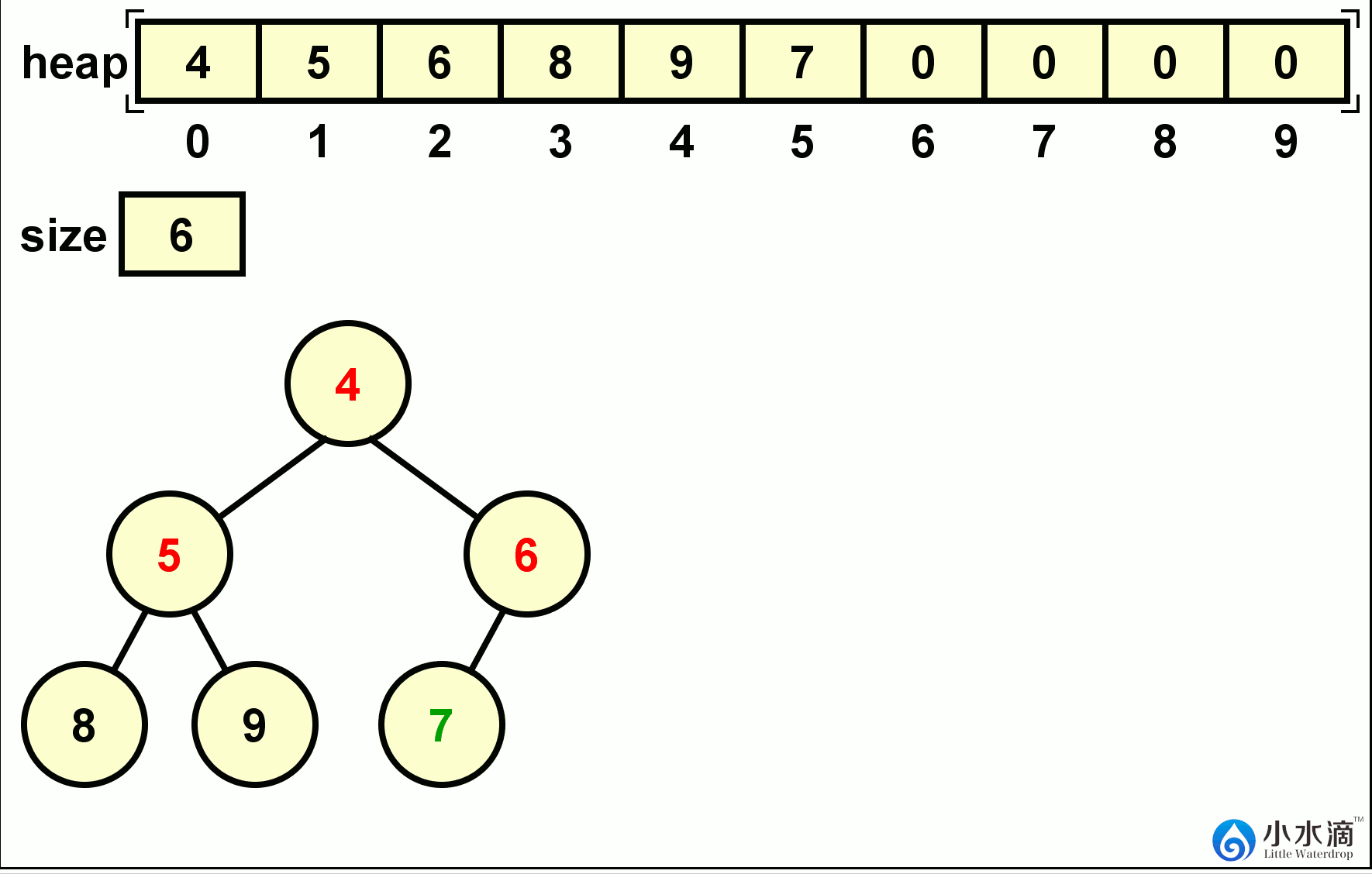
      avatar

      下面给出的是最小堆（MinHeap）插入操作的代码。因为插入操作是将一个新元素插入一个堆的最后，即在整个堆中，仅有该元素可能违反堆的性质。算法只需查找其父节点（用前面定义的getParentIndex方法）的元素值，如果新元素较小则交换位置（最小树）。交换位置后再继续比较新位置的父节点的元素值，如果新元素仍较小则继续交换位置。重复此步骤直到插入的新元素值大于其当前位置的父节点。

      public void insert(int e) {
    if(size >= maxSize) {
        System.out.println("Cannot insert since this heap is full.");
    } else {
        heap[size] = e;
        int currentIndex = size;
        size++;
        while (heap[currentIndex] < heap[getParentIndex(currentIndex)]) {
            int tmp = heap[currentIndex];
            int parentIndex = getParentIndex(currentIndex);
            heap[currentIndex] = heap[parentIndex];
            heap[parentIndex] = tmp;
            currentIndex = parentIndex;
        }
    }
}

    • 获取并删除当前堆顶节点。该节点即为堆的根节点，也是全堆中最小元素的节点（remove）

    该操作有两个作用，一是返回堆顶节点的元素值，二是将堆顶节点删除。因为删除堆顶节点影响堆的结构，所以有必要使用调整堆（heapify）的方法将其重新调整为一个堆。

    下面的代码给出了如何进行删除操作。首先将堆顶元素值（heap[0]）取出，再将堆的数组中的最后一个有效节点移动到堆顶变为新的堆顶节点。然后再调用调整堆方法（minHeapify）将其重新调整为堆。

    public int remove() {
  int result = heap[0];
  heap[0] = heap[size - 1];
  size--;
  minHeapify(0);
  return result;
}

    下面的动图给出了在一个堆中连续进行两次remove操作的例子。

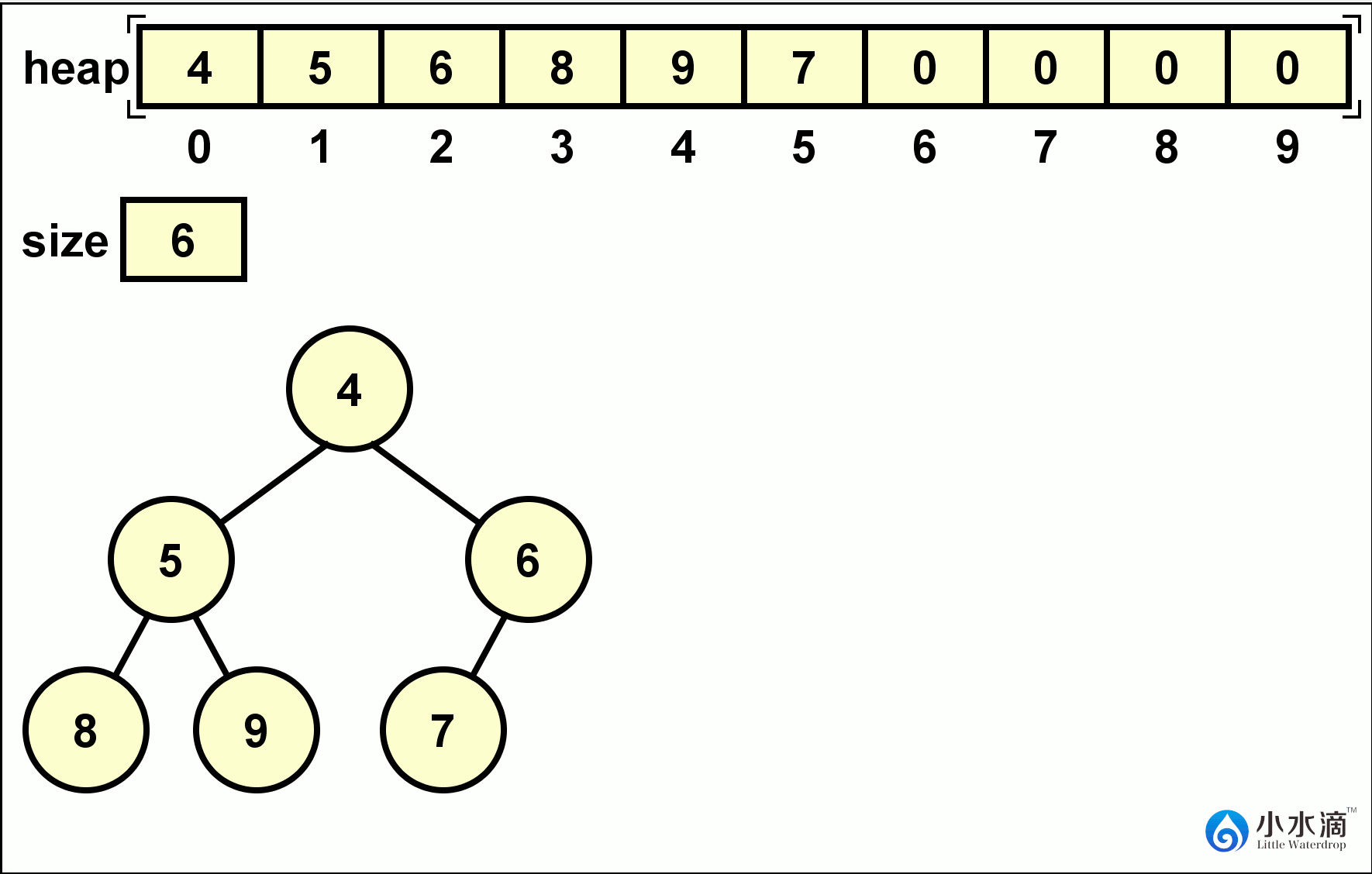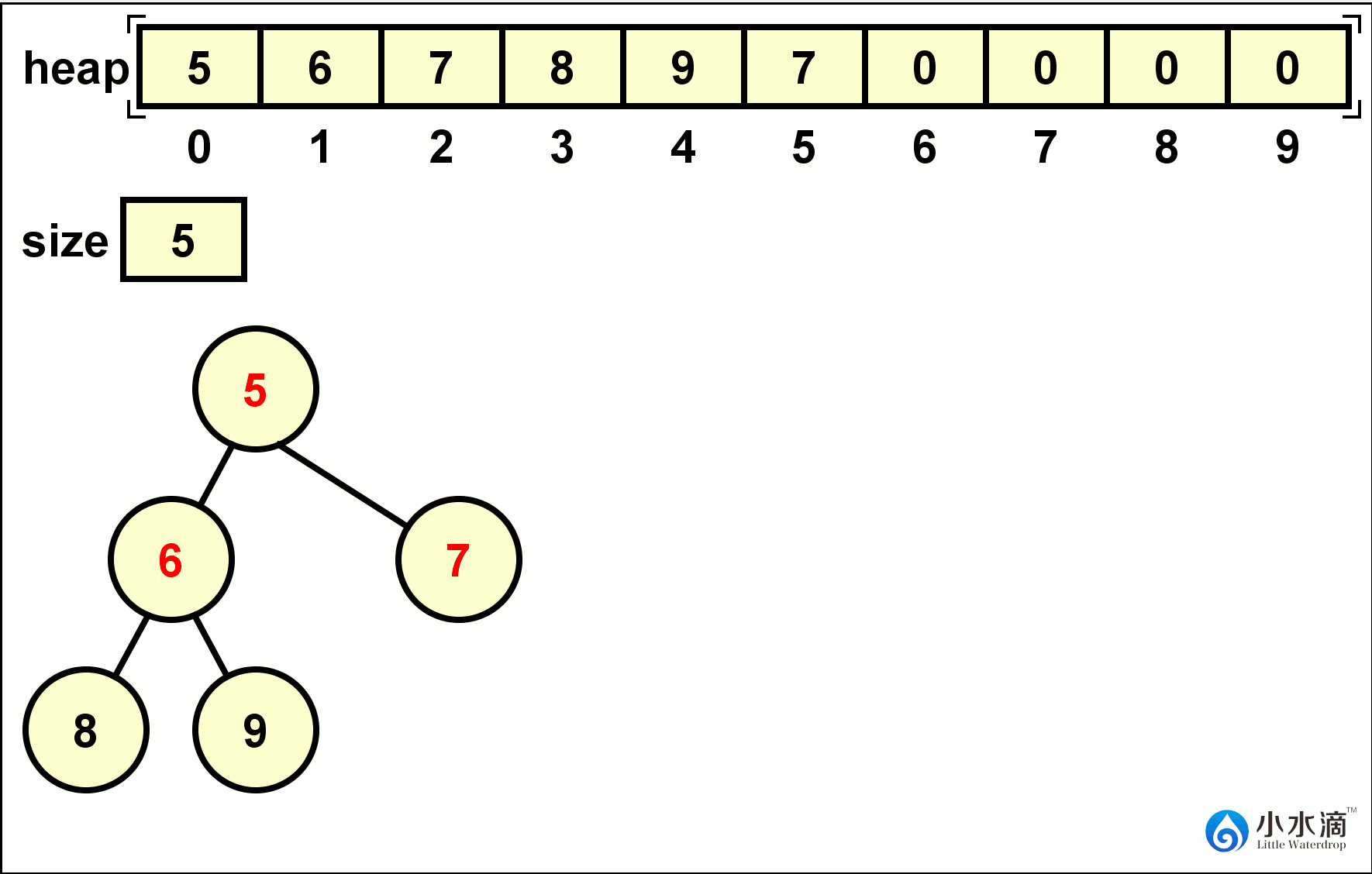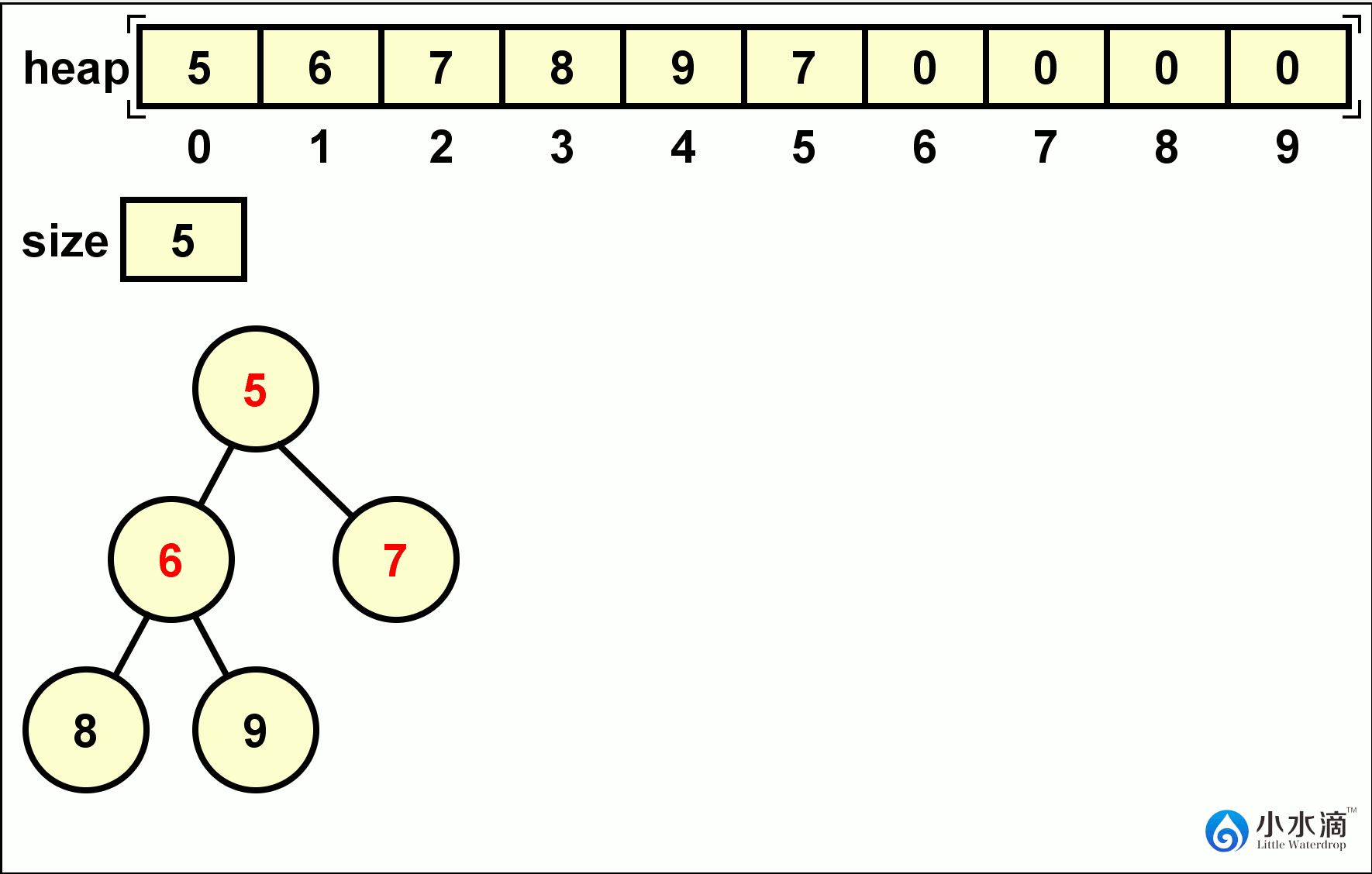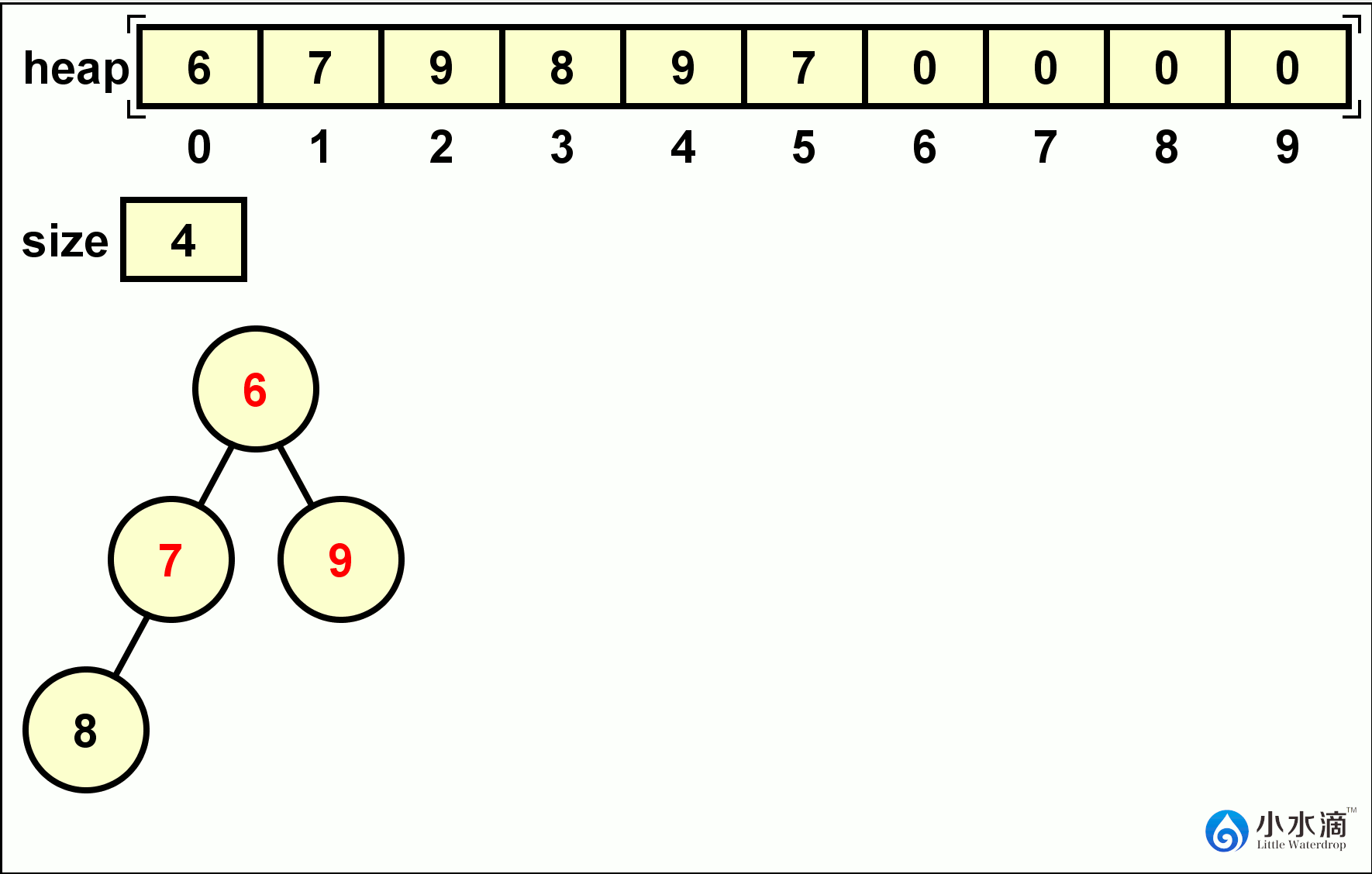
    avatar

  • 将删除堆顶节点的堆再度调整成最小堆（minHeapify）

    在前面的remove操作里调用了最小堆的调整算法（minHeapify）。需要注意的是调整算法并不能将任意的完全二叉树调整为堆。它只能将一个除了根节点，其他所有性质均满足堆定义的结构调整为堆。这个结构实际上出现在remove操作过程中：当删除堆顶节点后，该堆数组的最后一个有效元素被移至堆顶，那么此时的完全二叉树结构便可以用minHeapify调整为堆。

    下面给出了最小堆的调整方法（minHeapify）的递归实现。

    public void minHeapify(int position) {
    // 获取左右子节点在数组中的索引值（index）。
    int left = getLeftChildIndex(position);
    int right = getRightChildIndex(position);
    int smallest = -1;

    // 找出在当前节点和左右子节点中元素值最小的节点索引。
    if (left <= size - 1 && heap[left] < heap[position]) {
        smallest = left;
    } else {
        smallest = position;
    }

    if (right <= size - 1 && heap[right] < heap[smallest]) {
        smallest = right;
    }

    // 如果最小的节点不是当前节点，则将其与当前节点进行互换。
    if (smallest != position) {            
        int tmp = heap[position];
        heap[position] = heap[smallest];
        heap[smallest] = tmp;
        minHeapify(smallest);
    }
}

2. 优先队列（Priority Queue）

在优先队列中，每个元素都有各自的优先级。根据不同的优先级来决定元素获取服务的顺序。优先队列一般通过堆来实现。在下面的例子中，我们假设元素值越小，优先级越高。因此我们可以用上面的最小堆来实现该优先队列。

有了上面的最小堆代码，我们可以轻易的实现这个简单的优先队列。

查看和下载源代码 
public class PriorityQueue {
    MinHeap q = new MinHeap();

    public void enqueue(int e) {
        q.insert(e);
    }

    public int dequeue() {
        // 总是将优先级最高的元素出队，所以出队方法没有参数。
        return q.remove();
    }
}

当我们按顺序将优先级为5，3，1，4，2的五个任务依次入队，再连续出队五次。如下面的代码所示。

public class TestPriorityQueue {
    public static void main(String[] args) {
        PriorityQueue pq = new PriorityQueue();
        pq.enqueue(5);
        pq.enqueue(3);
        pq.enqueue(1);
        pq.enqueue(4);
        pq.enqueue(2);

        System.out.println(pq.dequeue());
        System.out.println(pq.dequeue());
        System.out.println(pq.dequeue());
        System.out.println(pq.dequeue());
        System.out.println(pq.dequeue());
    }
}

上面的代码输出结果如下。即不管入队的顺序如何，出队的顺序总是基于优先级的值。

1

2

3

4

5

 

上一章
下一章

注册用户登陆后可留言

Copyright  2019 Little Waterdrop, LLC. All Rights Reserved.