数据结构与算法

第十一章 动态规划（Dynamic Programming or DP）

• 1. 什么是动态规划

• 2. 斐波那契数列(Fibonacci Number)

   

1.什么是动态规划

• 介绍

  动态规划是一种强大且通用的算法设计技术，由理查德贝尔曼在20世纪50年代发明。比如动态规划在寻找最短路径算法中非常常见。动态规划类似于更有效的穷举搜索。不同的是穷举搜索的时间复杂度在指数级，而动态规划算法通常能在多项式时间内完成。可以将动态规划理解为一种谨慎且更有效的暴力搜索算法:

  动态规划 ≈ 谨慎的暴力搜索

  其实动态规划的思路非常简单。具体来说，动态规划将需要解决的问题划分为子问题，解决子问题，再用重用解决子问题的方法。所以也可以这样理解:

  动态规划 ≈ 子问题 + 重用

  动态规划不能解决所有的问题，但是许多复杂问题的唯一已知的多项式时间级算法都是基于动态规划的。

2. 斐波那契数列(Fibonacci Number)

• 递归版本

  在递归章节中我们已经介绍了斐波那契数列。简单回顾一下斐波那契数列中的数字 F_n 是由下面的公式计算的

  

  在递归章节中也介绍了最直接的求斐波那契数F_n的递归实现。

    public static int fibonacci(int n){
        if(n == 0){
            //基本情况1
            return 0;
        }
        else if(n == 1){
            //基本情况2
            return 1;
        }
        else{
            //递归情况
            return fibonacci(n-1) + fibonacci(n-2);
        }
    }
  

  这是一个正确的斐波那契数计算方法，却不是一个好的算法。它的时间复杂度是指数级的。我们现在简单的分析一下计算F_n所需要的时间T(n)。根据斐波那契数的定义，T(n)的计算时间等于T(n-1)与T(n-2)之和加上其他计算(比如检查n是否等于0或1)所消耗的时间常量 Θ(1)。

  

  因为 T(n-1) ≥ T(n-2) 且 Θ(1) 为常量，所以我们可以给根据下限将上式可以化简为

  

  因为 T(n-2) 需要递归ⁿ⁄₂次从而达到递归的基本条件(base case)，所以

  

  由此可见，基本的递归求斐波那契数的时间复杂度高达。

• memo版本 下图说明了递归求fibonacci(5)的过程。计算顺序是对该树的中序遍历搜索（In-Order Traversal，即从左到右的深度遍历搜索，具体见二叉树一章）。在递归过程中产生了大量的重复计算（下图中标红的部分）。如果能够记录下前面的计算结果并在后面的计算中直接引用而不是重新计算，就能够节省大量的时间。在memo版本的动态规划中，我们创建一个叫做memo的字典用来存储之前的结果。

  

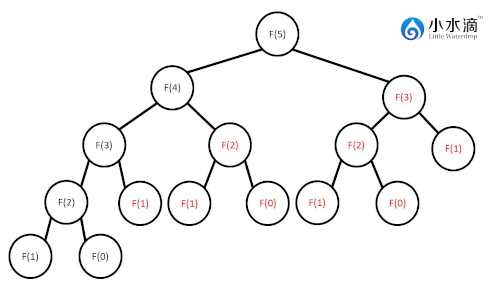
  下面我们用动态规划来实现斐波那契数的计算。首先创建一个字典(dictionary)，每算出一个斐波那契数，就将其放入字典(即一个memo)。每需要算一个斐波那契数，先检查是否已在字典里。如果已经在字典中，我们可以“重用”之前的结果来节省后面的计算。下面给出了一个计算前20个斐波那契数的完整Java程序。

  import java.util.HashMap;
  public class FibonacciDynamicProgramming {
      //用HashMap创建一个字典memo
      public static HashMap<Integer, Integer> memo = new HashMap<Integer, Integer>();
  
      public static int fibonacciNumberMemo(int n) {
          //如果F(n)已经在字典中，直接返回F(n)的值
          if(memo.containsKey(n)) 
              return memo.get(n);
          //基本情况(base case)，F(0)=0, F(1)=1
          if(n == 0||n==1) 
              return n;
          //递归计算
          int f_n = fibonacciNumberMemo(n - 1) + fibonacciNumberMemo(n - 2);
          //将计算出的值F(n)与n一起存入字典
          memo.put(n, f_n);
          return f_n;
      }
      public static void main(String[] args){
          for(int i = 0; i<20; i++){
              System.out.println(i+", "+fibonacciNumberMemo(i));
          }
      }
  }
  

  在动态规划的算法中，计算时间=子问题的数量×子问题的计算时间。注意此处，因为子问题的计算中重复出现的F(n)可以直接从字典中取得，所以不再有递归的时间消耗。所以子问题的计算时间为常量。即计算F(n)的时间消耗为

  

  所以动态规划记住并且重用子问题的解答来帮助解决整个问题。

• 自下而上版本(bottom-up)

  下面我们给出了用自下而上的动态规划来实现的计算斐波那契数的方法。这个方法与memo方法非常相似只是不使用递归。在这个自下而上的动态规划版本中，我们使用数组记录子问题的解答。数组的内容从n=0开始填充，即当计算F(n)的时候，F(0)到F(n-1)内容已经确保填充进了数组。所以此方法被称为自下而上的方法。此方法时间复杂度也为 Θ(n) 且不需要递归，所以真实时间消耗可能还要小于memo版本。

  public static int fibonacciNumberBottomUp(int n) {
      if(n==0||n==1)
          return n;
      int fib[] = new int[n + 1];
      fib[0] = 0;
      fib[1] = 1;
  
      for (int i = 2; i < n + 1; i++) {
          fib[i] = fib[i - 1] + fib[i - 2];
      }
      return fib[n];
  }