AVL树（AVL Tree）

• 1. AVL树的定义
• 2. AVL树的旋转
• 3. AVL树的实现

1. AVL树的定义

在学习二叉树的时候，我们介绍了一类特殊的二叉树：二叉搜索树。在二叉搜索树中查找一个元素的速度要远远快于普通二叉树。同时我们也注意到，如果二叉搜索树不平衡的话，将会极大的影响其搜索效率。

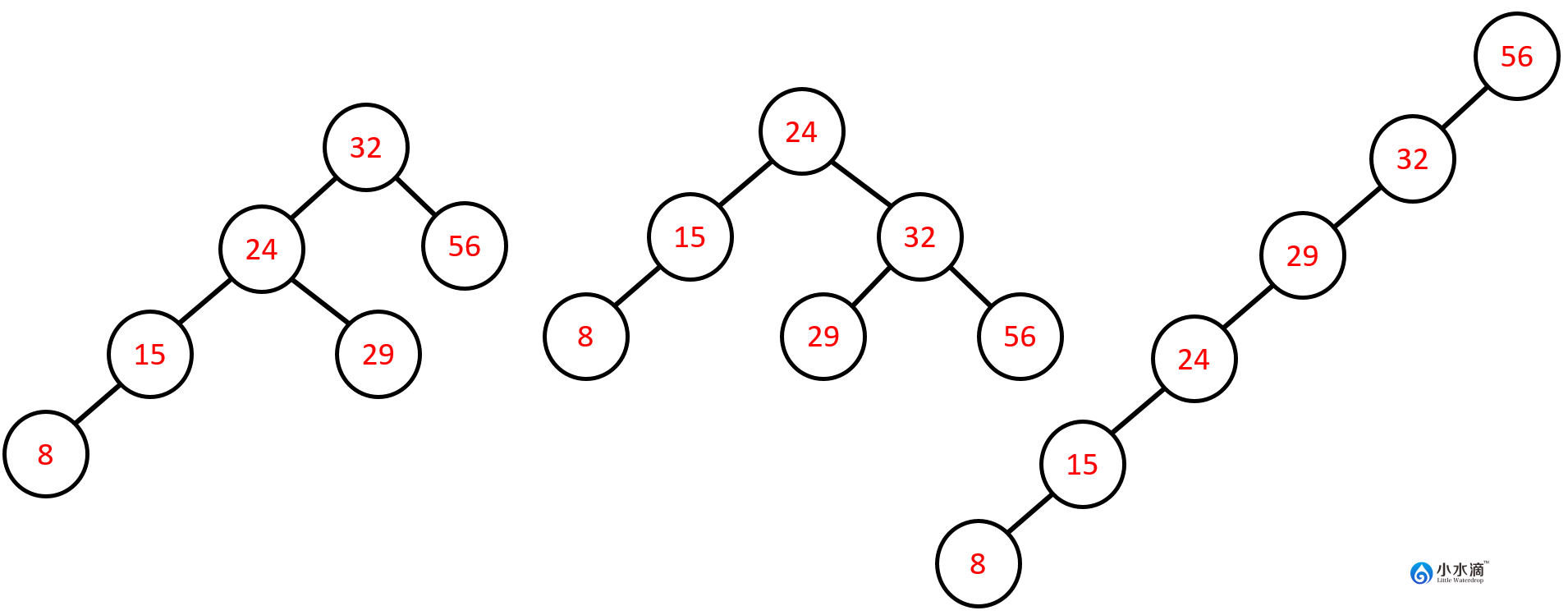
如果我们用下面的数字生成一棵二叉搜索树，基于不同的插入顺序，树形结构会有多种可能。

8, 15, 24, 29, 32, 56

在下图中，我们给出的都是基于上面数列的三种不同的二叉搜索树结构。从搜索效率上来看，中间的二叉搜索树效率最高，左边的次之，右边的最差。如果要查找元素8，中间的二叉搜索树只需要3次比较，左边的需要4次，右边需要6次。实际上右边的二叉搜索树已经相当于一个单链表结构。由此可见，要提高二叉搜索树的效率，需要在节点数量一定的情况下尽可能的减少二叉搜索树的层级结构。从三个二叉搜索树的例子来看，如果能减少左右子树的高度差，就能有效减少二叉搜索树的层数。如果任意节点对应的两棵子树的高度差都不大于一，我们称这是一个平衡的二叉搜索树。

AVL树就是带有自平衡功能的二叉搜索树。AVL树得名于它的发明者G. M. Adelson-Velsky和Evgenii Landis的姓氏缩写。AVL树使用平衡因子（Balance Factor）来判断树是否平衡。一个节点的平衡因子为其左子树高度减去右子树高度。当一个节点的平衡因子为1，-1，或0时，此节点被认为是平衡的。

同样地，以上图为例，左边的二叉搜索树的根节点32的左子树高度为3，右子树高度为1，所以节点32不是平衡节点。而中间的二叉搜索树的每个节点的平衡因子的值都在1，-1，或0之中，因此中间为一个平衡的二叉搜索树。

2. AVL树的旋转

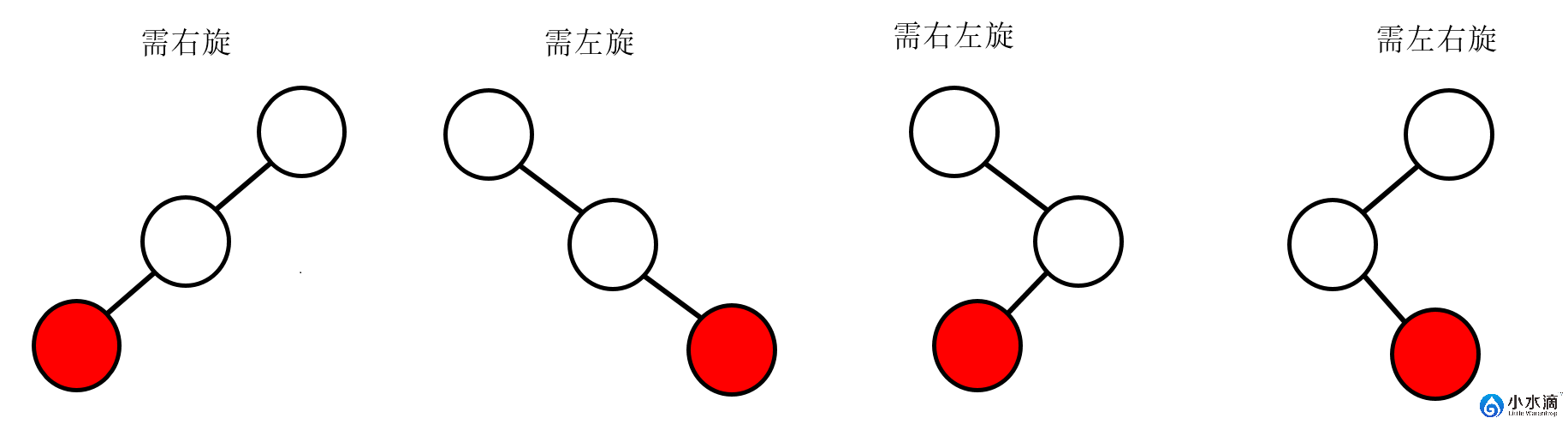
因为AVL树本质上也是二叉搜索树，因此其操作和二叉搜索树类似。只是为了保证其平衡性，在改变树结构的操作之前或者之后需要进行AVL旋转（AVL Rotation）。AVL树共有如下四种旋转方式。因为在生成二叉搜索树的时候，插入节点的顺序会影响树结构，所以AVL树有必要在插入节点后进行相关调整从而保证树的平衡性。

下图给出的例子表示了四类导致不平衡的插入位置。针对不同位置需要不同的旋转操作。

1. 右旋

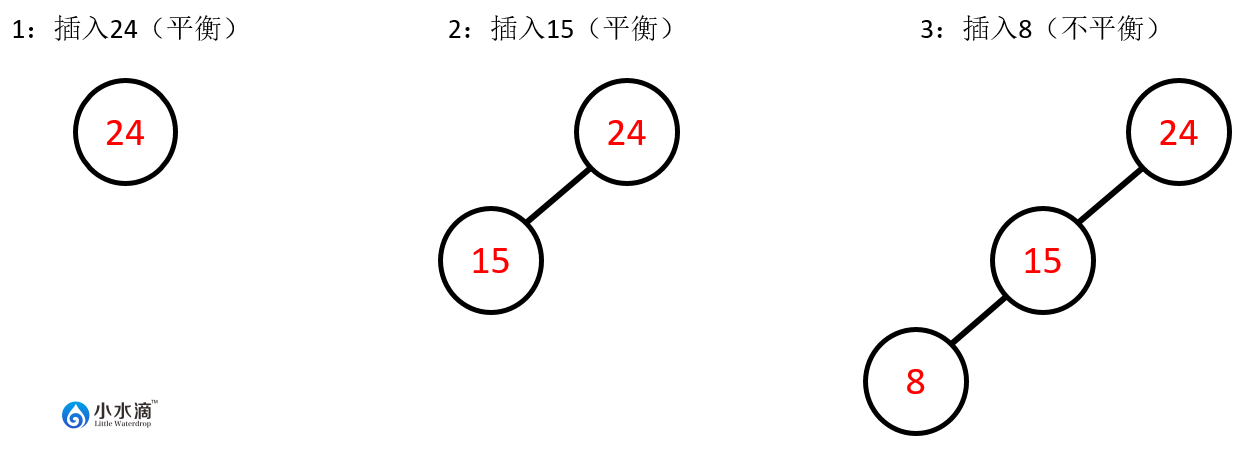
   如果按顺序将{24, 15, 8}3个元素插入一棵AVL树，每个元素插入的状态如下图所示。可以发现当插入8后，节点24的平衡因子变为 $（2-0)=2$，即该节点变为不平衡节点。

   

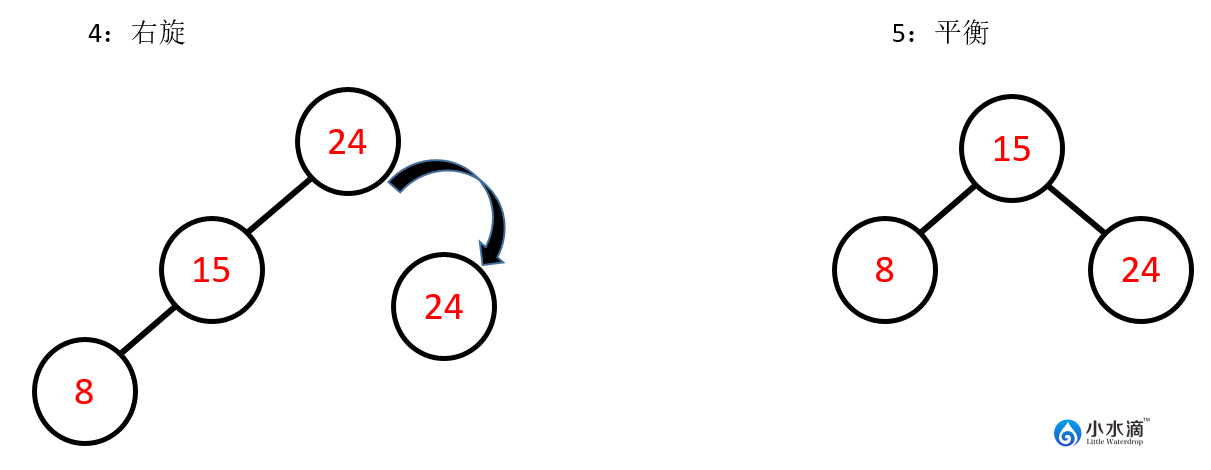
   因此，在完成此插入操作之前，还需要做以下步骤将其调整平衡，即对节点24进行右旋操作。

   

 

2. 左旋

   左旋操作跟右旋类似，在此只给出左旋操作的基本例子。

   如果按顺序将{8，15，24}3个元素插入AVL树，其状态如下图所示。可以发现当插入24后，节点8的平衡因子变为 $（0-2)=-2$，即该节点变为不平衡节点。

   

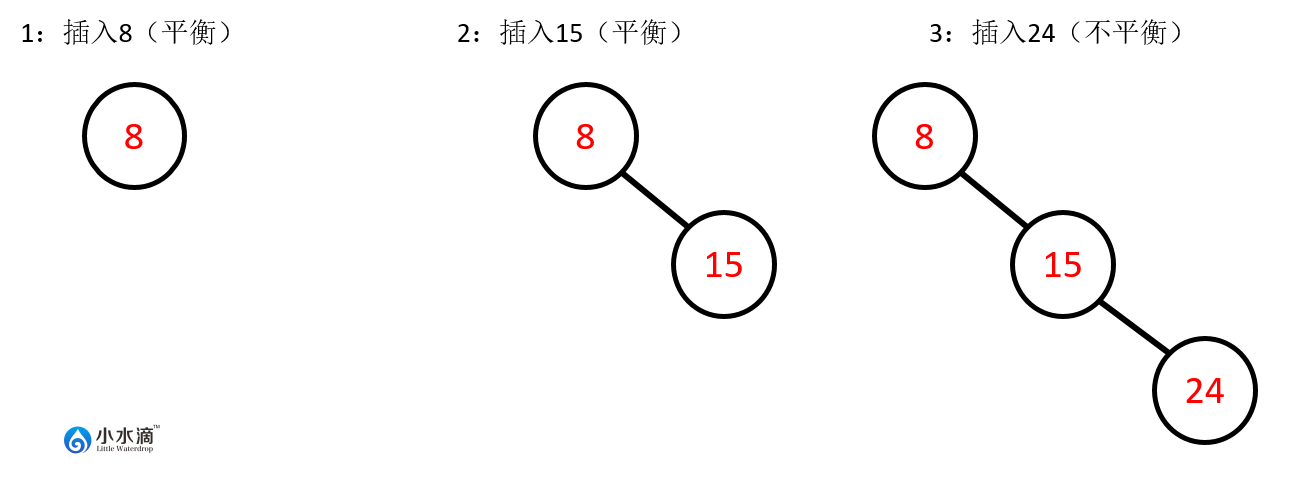
   因此，在完成此插入操作之前，还需要做以下步骤将其调整平衡，即对节点8进行左旋操作。

   

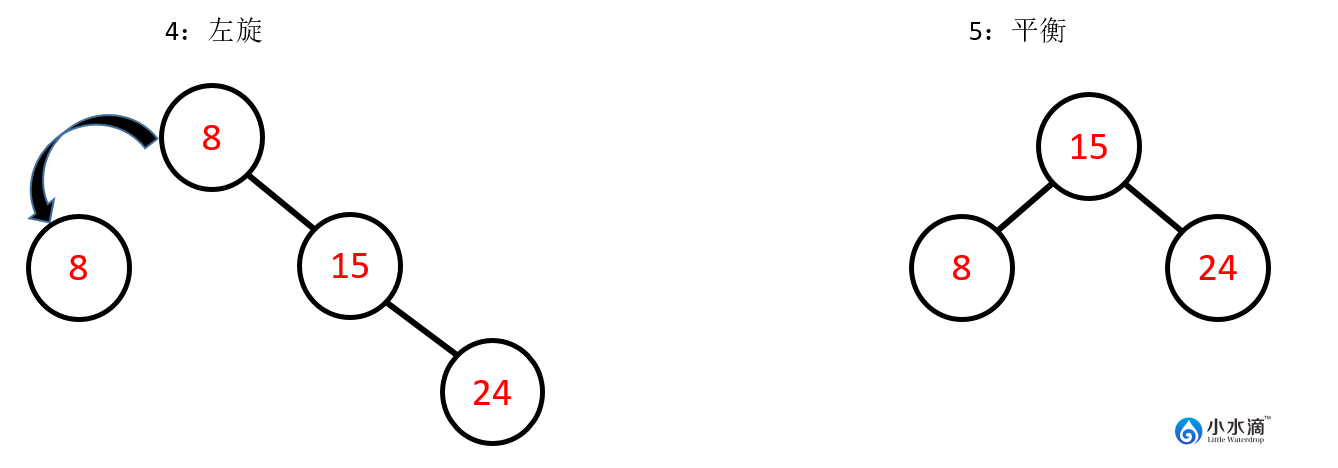
左旋和右旋操作都属于单次旋转的AVL树操作。

3. 右左旋

   如果按顺序将{8，24，15}3个元素插入AVL树，其状态如下图所示。可以发现当插入15后，节点8的平衡因子变为 $（0-2)=-2$，即该节点变为不平衡节点。

   

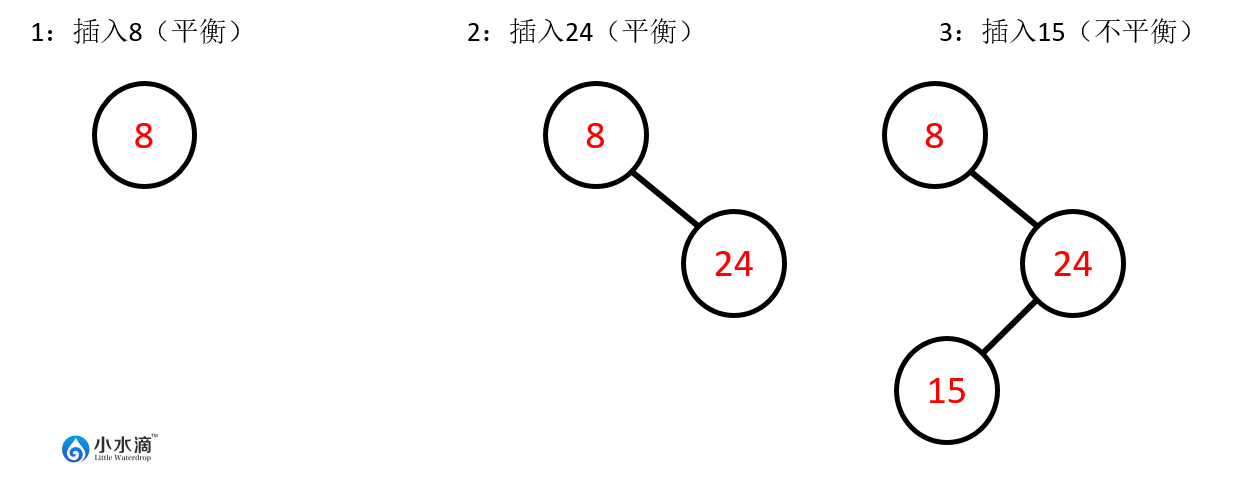
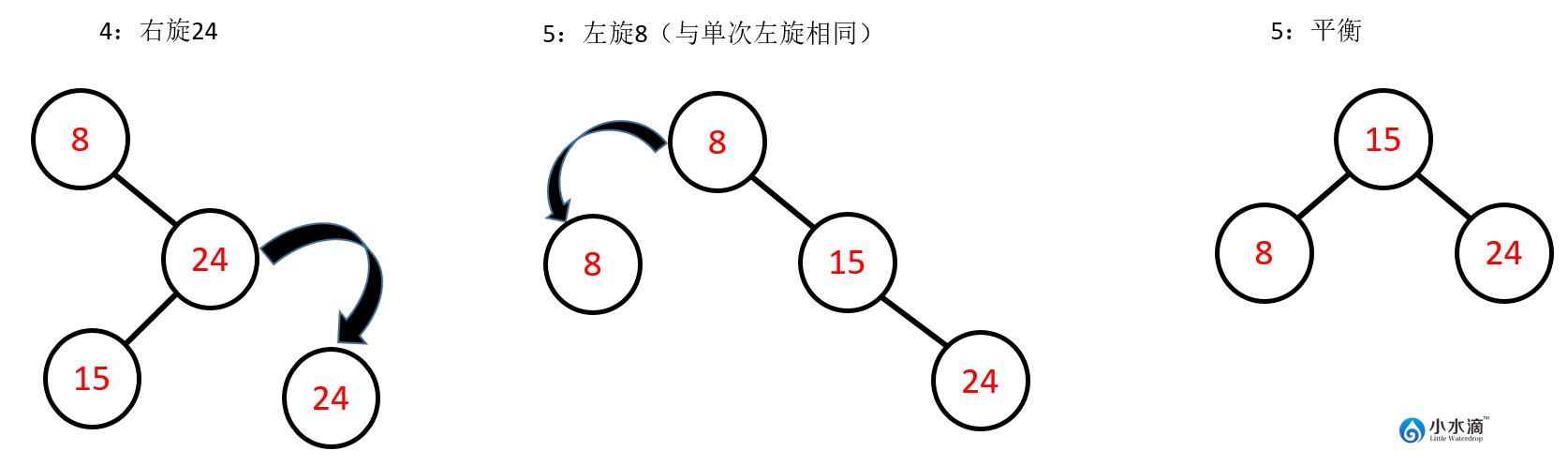
   因此，在完成此插入操作之前，还需要做以下步骤将其调整平衡。即先对节点24进行右旋操作，再对节点8进行左旋操作。

   

4. 左右旋

   如果按顺序将{24，8，15}3个元素插入AVL树，其状态如下图所示。可以发现当插入15后，节点24的平衡因子变为 $（0-2)=-2$，即该节点变为不平衡节点。

   

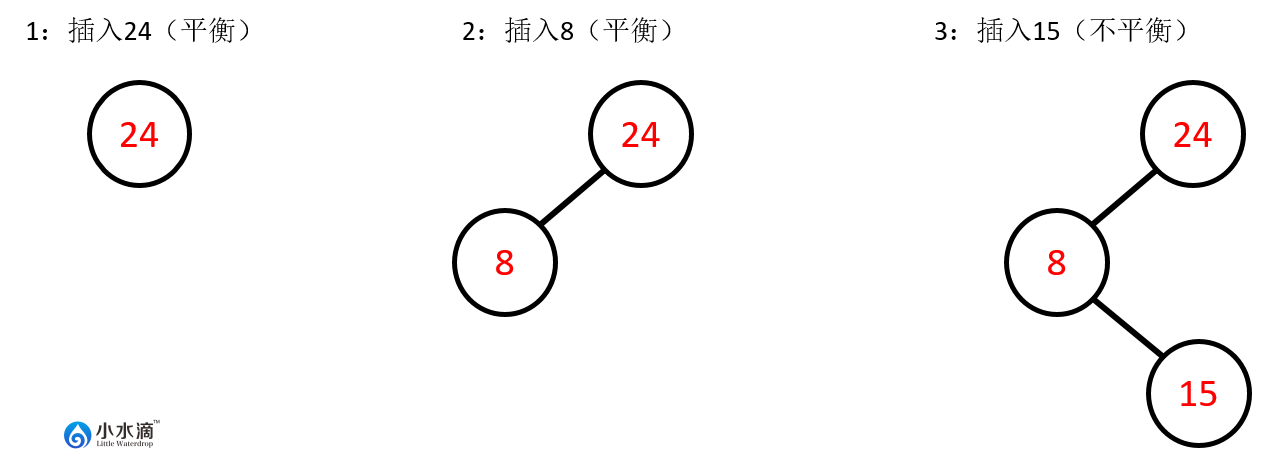
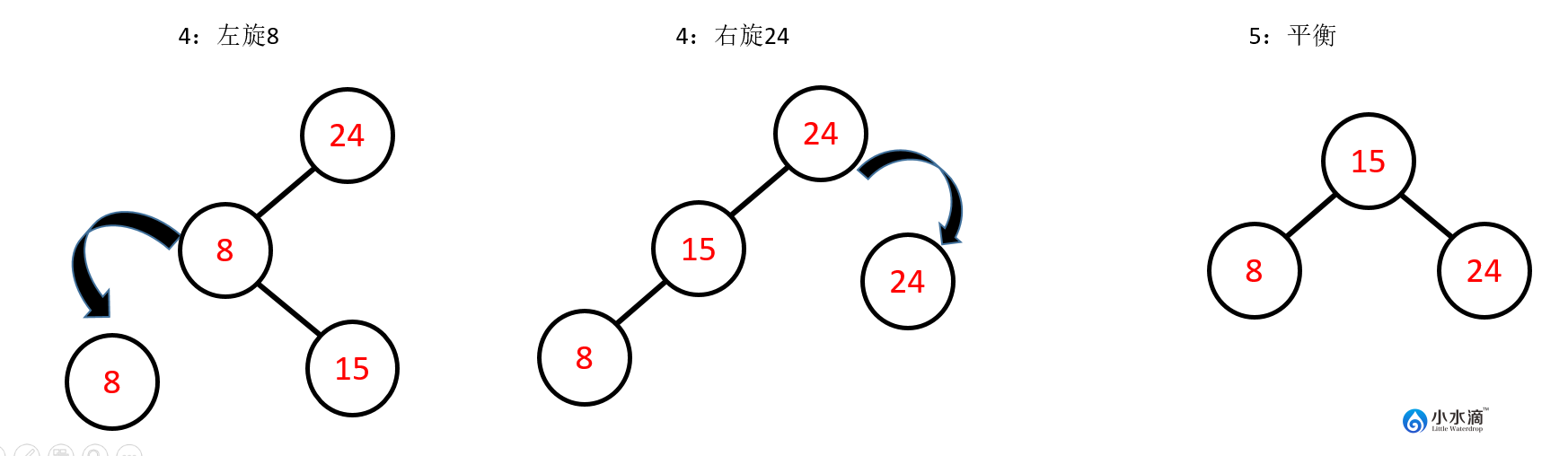
   因此，在完成此插入操作之前，还需要做以下步骤将其调整平衡。即先对节点8进行左旋操作，再对节点24进行右旋操作。

   

 

3. AVL树的实现

下图是一个更复杂的右旋例子，在一个已经平衡的AVL树中插入8。节点32的平衡因子变为 $(3-1)=2$，不平衡。

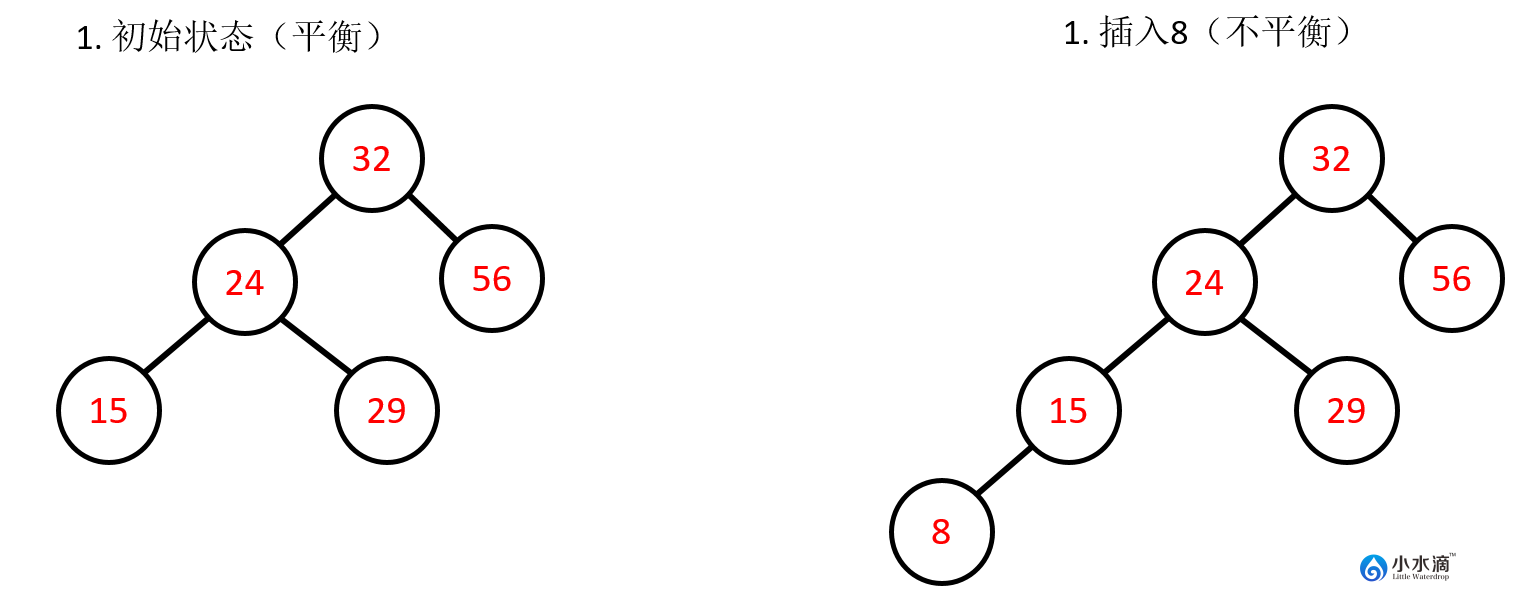
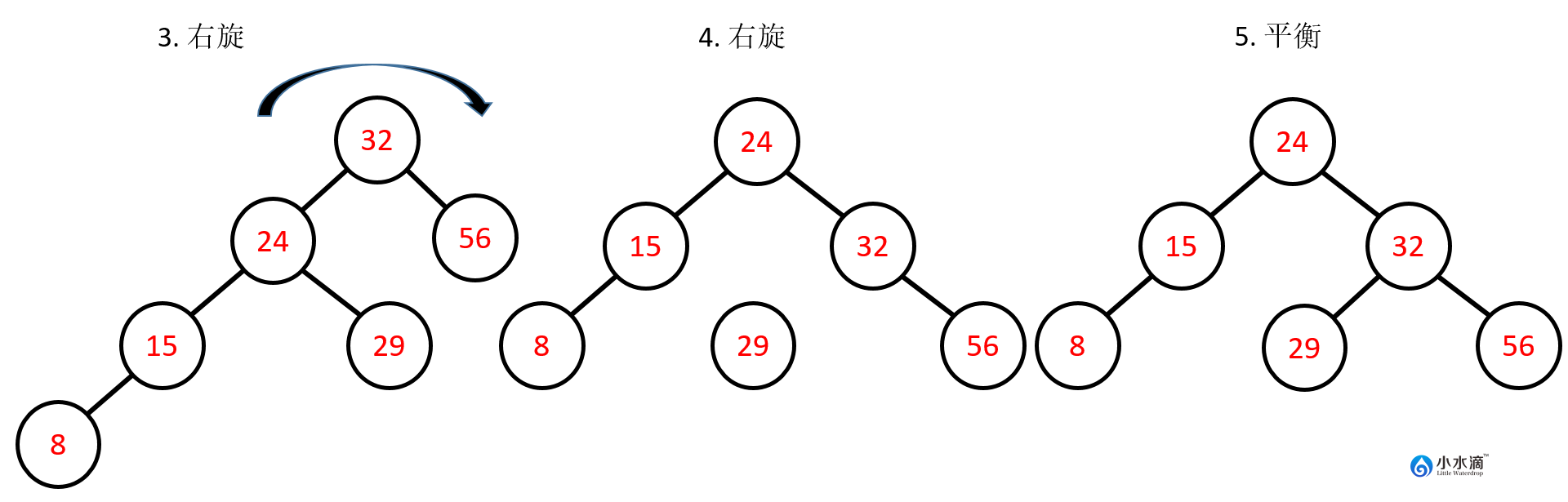
因此需要对节点32进行右旋操作。在下图中，32变为其左子节点24的右子节点。注意24本来的右子节点29变为了32的左子节点。

通过上例我们能看出AVL树旋转的情况可能很复杂，前一小节中的图都是最简单的情况。我们下面的图示可以用来表示更通用的例子。这些图可以帮助我们具体实现相关的代码。

下图是几个更复杂的旋转示意图。在这些图中，T表示不平衡的节点，S表示T的左子节点，A和B为S节点的左右子树，C为T节点的右子树，圆圈表示节点，三角表示子树。

AVL树节点在二叉搜索树节点类的基础上增加了height（高度）属性用来计算平衡因子（Balance Factor）。

class Node {
    int element;
    int height;
    Node left;
    Node right;
}

1. 右旋

   下图可以涵盖所有的右旋情况。T的平衡因子为其左子树高度减右子树高度。图中的虚线表示出左子树高度比右子树高2，所以平衡因子为 $2$，因此需要右旋。右旋的结果为T的左子树变为B，S的右子树变为T。上述操作均反映在下面的代码里。

   

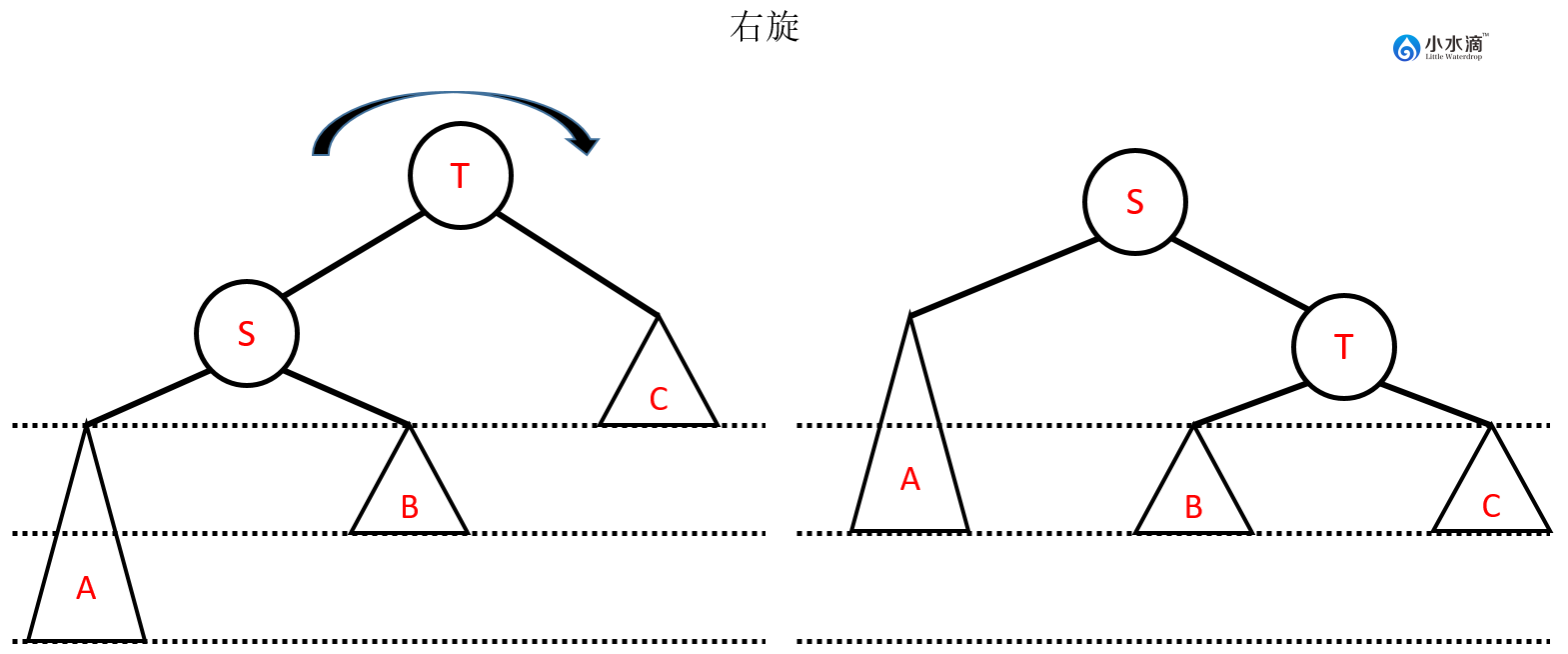
   Node rightRotate(Node t) { 
       Node s = t.left; 
       Node b = s.right; 
   
       s.right = t;
       t.left = b;
   
       return s;
   } 
   

2. 左旋

   下图可以涵盖所有的左旋情况。T的平衡因子为其左子树高度减右子树高度。图中的虚线表示出左子树高度比右子树低2，所以平衡因子为 $-2$。因此需要左旋。左旋的结果为S的左子树变为T，T的右子树变为B。

   

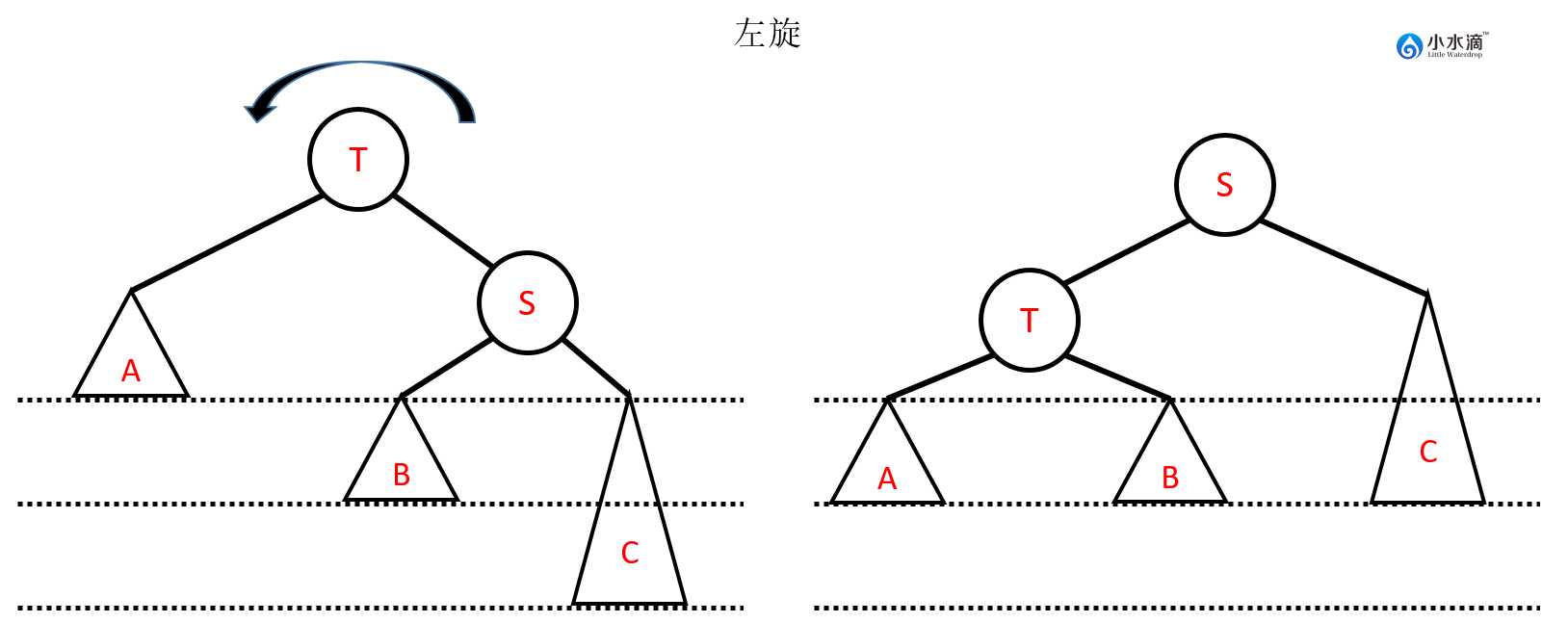
   Node rotateLeft(Node t) {
       Node s = t.right;
       Node b = s.left;
       s.left = t;
       t.right = b;
   
       return s; 
   }
   

3. 右左旋

   下图可以涵盖所有的右左旋情况。注意右旋和左旋的位置。

   

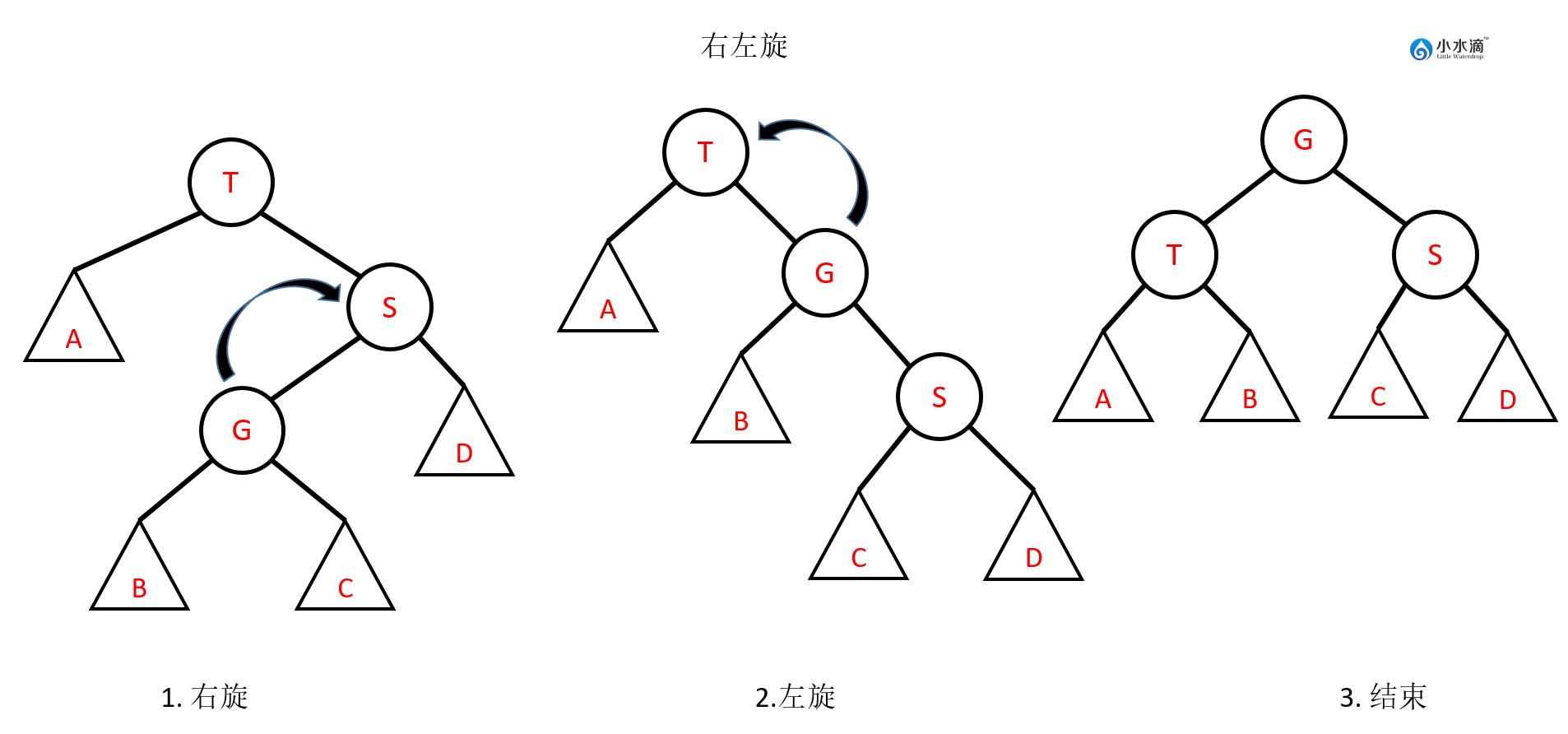
   反映在函数里，右左旋操作上分为两步。首先在当前节点的右子节点右旋，再在当前节点左旋。

   Node rotateRightLeft(Node t) {
       Node s = t.right;
       t.right = rotateRight(s);
   
       return rotateLeft(t);
   }
   

4. 左右旋

   下图可以涵盖所有的左右旋情况。注意左旋和右旋的位置。

   

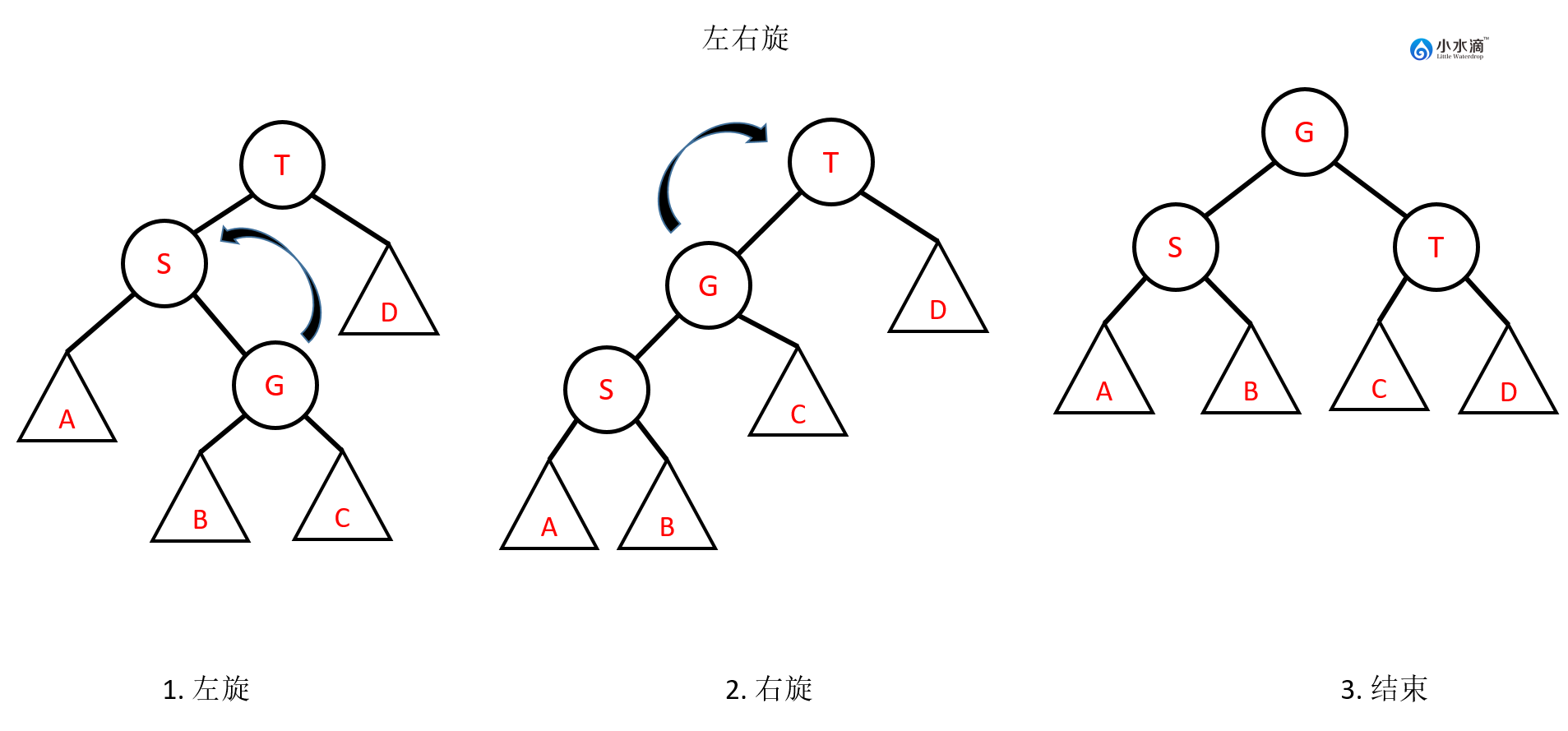
   反映在函数里，左右旋操作上分为两步。首先在当前节点的左子节点左旋，再在当前节点右旋。

   Node rotateLeftRight(Node t) {
       Node s = t.left;
       t.left = rotateLeft(s);
   
       return rotateRight(t);
   }